中考数学复习-几何综合复习卷

更新时间：2024-09-22 浏览次数：1 类型：复习试卷

一、单选题（每题3分，共30分）

1. (2024八下·丰都县期中) 下列命题中，真命题是（）

A . 对角线相等的四边形是矩形 B . 一组对边平行，另一组对边相等的四边形是平行四边形 C . 对角线互相垂直平分的四边形是菱形 D . 一组邻边相等，并且有一个内角为直角的四边形是正方形

答案解析收藏纠错 + 选题
2. (2024九下·松原模拟) 如图，已知直线 $\text{[math]}$ ，现将含 $\text{[math]}$ 角的直角三角板放入平行线之间，两个锐角顶点分别落在两条直线上．若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021七上·慈溪期末) 如图，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上， $\text{[math]}$ ，那么下列说法错误的是（）

A . $\text{[math]}$ 与 $\text{[math]}$ 相等 B . $\text{[math]}$ 与 $\text{[math]}$ 互余 C . $\text{[math]}$ 与 $\text{[math]}$ 互补 D . $\text{[math]}$ 与 $\text{[math]}$ 互余

答案解析收藏纠错 + 选题
4. (2023七下·赤峰期末) 如图，AB∥CD ， ∠BED=110°，BF平分∠ABE，DF平分∠CDE，则∠BFD= ( )

A . 110° B . 115° C . 125° D . 130°

答案解析收藏纠错 + 选题
5. (2024六下·招远期末) 如图所示，∠BAC=90°，AD⊥BC于D，则下列结论中：①AB⊥AC；②AD与AC互相垂直；③点C到AB的垂线段是线段AB；④点A到BC的距离是线段AD的长度；⑤线段AB的长度是点B到AC的距离；⑥线段AB是点B到AC的距离．其中正确的有(　　)．

A . 3个 B . 4个 C . 5个 D . 6个

答案解析收藏纠错 + 选题
6. (2020七下·恩施期末) 如图：有两条平行小路 $\text{[math]}$ ，这两条小路分别与一条公路 $\text{[math]}$ 在 $\text{[math]}$ 两处相交，并且相交的角度 $\text{[math]}$ ，现在想经过 $\text{[math]}$ 处修一条水渠，使水渠与公路平行，那 $\text{[math]}$ 的度数应该是（）

A . 120° B . 30° C . 60° D . 80°

答案解析收藏纠错 + 选题
7. (2019七下·广州期中) 将一副三角板ABC如图放置，使点A在DE上，BC//DE，其中，则∠E=30°，则∠AFC的度数是（）

A . 45° B . 50° C . 60° D . 75°

答案解析收藏纠错 + 选题
8. (2023·徐汇模拟) 下列命题中假命题是（）

A . 任意两个等腰直角三角形都相似 B . 任意两个含36°内角的等腰三角形相似 C . 任意两个等边三角形都相似 D . 任意两个直角边之比为1：2的直角三角形相似

答案解析收藏纠错 + 选题
9. (2023七下·怀远期末) 将图1中周长为32的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形，并将它们按图2的方式放入周长为48的长方形中，则没有覆盖的阴影部分的周长为（）

A . 16 B . 24 C . 30 D . 40

答案解析收藏纠错 + 选题
10. (2021七上·路北期中) 如图，在数轴上，点A表示1，现将点A沿数轴做如下移动：第一次将点A向左移动3个单位长度到达点A₁ ，第二次将点A向右移动6个单位长度到达点A₂ ，第三次将点A₂向左移动9个单位长度到达点A₃ ，按照这种移动规律移动下去，第n次移动到点A_n ，如果点A_n与原点的距离不小于20，那么n的最小值是（　　）

A . 12 B . 13 C . 14 D . 15

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分）

11. (2023七上·期末) 若∠α=30.2°，则∠α的补角度数为(用“°、'”表示)．

答案解析收藏纠错 + 选题
12. (2020七上·孝南期中) 在数轴上，与表示数-2的点距离是3的点所表示的数是.

答案解析收藏纠错 + 选题
13. (2020九上·泰山期末) 如图，将周长为10的 $\text{[math]}$ 沿 $\text{[math]}$ 边向右平移4个单位，得到 $\text{[math]}$ 则四边形 $\text{[math]}$ 的周长为．

答案解析收藏纠错 + 选题
14. (2023七下·安溪期末) 在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ．如图1，点 $\text{[math]}$ 与点 $\text{[math]}$ 重合，点 $\text{[math]}$ 在边 $\text{[math]}$ 上．如图2，将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，边 $\text{[math]}$ 与边 $\text{[math]}$ 分别交于点 $\text{[math]}$ 时，连接 $\text{[math]}$ ．下列4个以下结论：

① $\text{[math]}$ ；
②当 $\text{[math]}$ 时， $\text{[math]}$ ；
③当 $\text{[math]}$ 时， $\text{[math]}$ ；
④当 $\text{[math]}$ 时， $\text{[math]}$ 为定值．
其中正确的是．（写出所有正确结论的序号）

答案解析收藏纠错 + 选题
15. (2023六下·牟平期末) 如图，一束光沿 $\text{[math]}$ 方向，先后经过平面镜 $\text{[math]}$ 反射后，沿E方向射出，已知 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2021七下·通河期末) 如图，已知 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 为 $\text{[math]}$ 上的两点， $\text{[math]}$ 、 $\text{[math]}$ 为 $\text{[math]}$ 上的两点，延长 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，且 $\text{[math]}$ 平分 $\text{[math]}$ ，若 $\text{[math]}$ ．则下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④设 $\text{[math]}$ ， $\text{[math]}$ ；⑤ $\text{[math]}$ 的度数为50°．其中正确结论为．（填序号）

答案解析收藏纠错 + 选题

三、作图题（共2题，共16分）

17. (2019七上·惠山期末) 在如图所示的方格纸中，每个小正方形的边长为1，每个小正方形的顶点都叫做格点．已知三角形ABC的三个顶点都在格点上．
1. （1）按下列要求画图：过点B和一格点D画AC的平行线BD，过点C和一格点E画BC的垂线CE，并在图中标出格点D和E；
2. （2）求三角形ABC的面积．
答案解析收藏纠错 + 选题
18. (2024七上·安顺期末) 如图，已知四点A、B、C、 $\text{[math]}$ ，请用尺规作图完成．（保留画图痕迹）
1. （1）画直线 $\text{[math]}$ ；
2. （2）画射线 $\text{[math]}$ ；
3. （3）连接 $\text{[math]}$ ；
4. （4）在线段 $\text{[math]}$ 上取点 $\text{[math]}$ ，使 $\text{[math]}$ 的值最小，你的依据是_▲_．
答案解析收藏纠错 + 选题

四、解答题（共7题，共62分）

19. (2024七下·纳溪期末) 已知：如图， $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 互余， $\text{[math]}$ 于点 $\text{[math]}$ ．求证： $\text{[math]}$
请将下面的推理过程补充完整．
证明：∵ $\text{[math]}$ （已知），
∴ $\text{[math]}$ （                       ），
∴ $\text{[math]}$                    $\text{[math]}$ ，
又∵ $\text{[math]}$ 和 $\text{[math]}$ 互余（已知），
∴ $\text{[math]}$                   ，
∴ $\text{[math]}$                       （                   ），
∵ $\text{[math]}$ （已知），
∴ $\text{[math]}$ ，
∴ $\text{[math]}$ （                    ，两直线平行）．

答案解析收藏纠错 + 选题
20. (2024七下·泌阳月考) 如图， $\text{[math]}$ ， $\text{[math]}$ 是截线， $\text{[math]}$ ， $\text{[math]}$ ，求： $\text{[math]}$ 的度数．

答案解析收藏纠错 + 选题
21. (2022七上·内江期末) 如图，如果AB//CD， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ， $\text{[math]}$ .试说明：AD//BC.

答案解析收藏纠错 + 选题
22. (2020七上·五莲期末) 如图，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ．求 $\text{[math]}$ 的度数．

答案解析收藏纠错 + 选题
23. (2024七下·永兴开学考) 如图1，点C在线段 $\text{[math]}$ 上，图中共有三条线段 $\text{[math]}$ 和 $\text{[math]}$ ，若其中有一条线段的长度是另外一条线段长度的2倍，则称点C是线段 $\text{[math]}$ 的“巧点”．
1. （1）若点C是线段 $\text{[math]}$ 的中点，判断C是否是线段 $\text{[math]}$ 的“巧点”；
2. （2）如图2，已知 $\text{[math]}$ ，动点P从点A出发，以2cm/s的速度沿AB向点B匀速运动；点Q从点B出发，以1cm/s的速度沿 $\text{[math]}$ 向点A匀速运动，点P，Q同时出发，设移动的时间为t（s），当其中一点到达终点时，运动停止．
  ①当t为何值时，P、Q重合？
  ②当t为何值时，Q为 $\text{[math]}$ 的“巧点”？
答案解析收藏纠错 + 选题
24. (2023七上·路北期末) 如图，数轴上两点 $\text{[math]}$ 所表示的数分别为 $\text{[math]}$ ，
1. （1）写出线段 $\text{[math]}$ 的中点 $\text{[math]}$ 所对应的数；
2. （2）若点 $\text{[math]}$ 从 $\text{[math]}$ 出发，以每秒 $\text{[math]}$ 个单位长度的速度向左运动，运动时间为 $\text{[math]}$ 秒：
  $\text{[math]}$ 用含 $\text{[math]}$ 的代数式表示点 $\text{[math]}$ 所对应的数；
  $\text{[math]}$ 当 $\text{[math]}$ 时，求 $\text{[math]}$ 值．
答案解析收藏纠错 + 选题
25. (2024七下·望城月考) 已知 $\text{[math]}$ ∥ $\text{[math]}$ ，点 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 上的两点，点 $\text{[math]}$ 在 $\text{[math]}$ 、 $\text{[math]}$ 之间，连接 $\text{[math]}$ 、 $\text{[math]}$ .
（1）如图①，若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
（2）如图②，若点 $\text{[math]}$ 是 $\text{[math]}$ 下方一点， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，已知 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
（3）如图③，若点 $\text{[math]}$ 是 $\text{[math]}$ 上方一点，连接、 $\text{[math]}$ ，且 $\text{[math]}$ 的延长线 $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.

答案解析收藏纠错 + 选题

五、实践探究题（共2题，共24分）

26. (2024七下·龙岗期中) 如图（a）所示，将一把含30°角的直角三角板ABC的BC边放置于长方形直尺DEFG的 $\text{[math]}$ 边上．
1. （1）填空： $\text{[math]}$ °， $\text{[math]}$ °．
2. （2）如图（b）所示，现把三角板绕点B逆时针旋转n°，当 $\text{[math]}$ ，且点C恰好落在DG边上时，① $\text{[math]}$ ▲ °， $\text{[math]}$ ▲ °；（结果用含n的代数式表示）
  ②若 $\text{[math]}$ 恰好是 $\text{[math]}$ 的 $\text{[math]}$ 倍，求n的值．
3. （3）如图（a）所示放置的三角板ABC ，现将射线BF绕点B以2°/s的速度逆时针旋转得到射线BM ，同时射线QA绕点Q以3°/s的速度顺时针旋转得到射线QN ，当射线QN旋转至与QB重合时，则射线BM ， QN均停止转动，设旋转时间为ts．
  ①在旋转过程中，若射线BM与射线QN相交，设交点为P ．当 $\text{[math]}$ 时，则 $\text{[math]}$ ▲ ．
  ②在旋转过程中，是否存在 $\text{[math]}$ ？若存在，求出此时t的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题
27.
1. （1）问题情境：
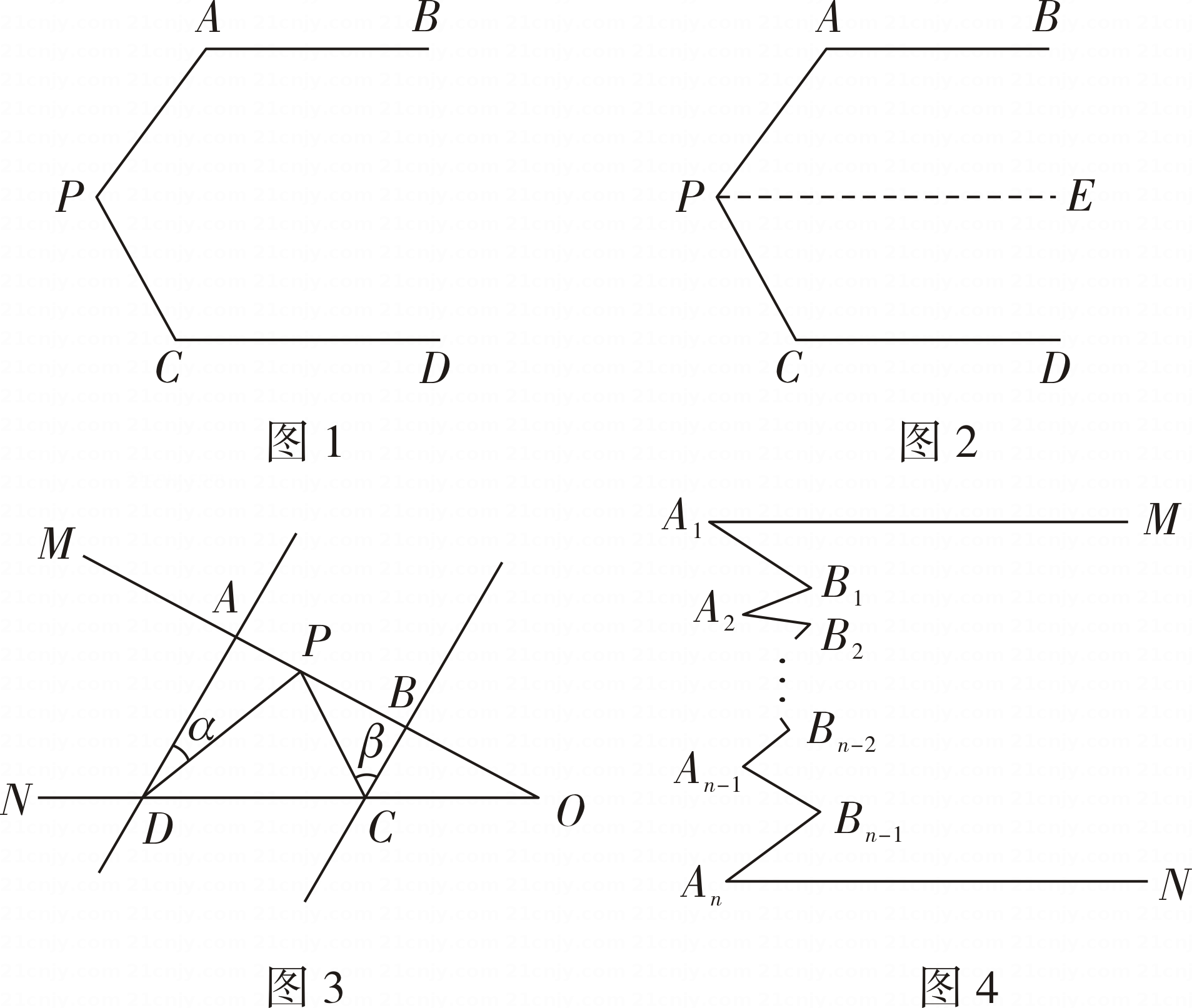
  如图1，已知 AB∥CD，∠APC=108°.求∠PAB+∠PCD的度数.
  经过思考，小敏提出思路：如图2，过点 P 作PE∥AB，根据平行线的有关性质，可得∠PAB+∠PCD= °.
2. （2）问题迁移：
  如图3，AD∥BC，点 P 在射线OM 上运动，∠ADP=α，∠BCP=β.
  当点 P 在A，B两点之间运动时，∠CPD，α，β之间有何数量关系? 请说明理由.
3. （3）当点 P 在A，B 两点外侧运动时（点 P 与点A，B，O不重合），请直接写出∠CPD，α，β之间的数量关系.
4. （4）问题拓展：
  如图4， $\text{[math]}$ -An是一条折线段.
  依据此图信息，把你所发现的结论用数学式子表达出来：
答案解析收藏纠错 + 选题