人教版数学九年级全册知识点训练营——旋转的奔驰模型及费马点模...

更新时间：2024-10-15 浏览次数：17 类型：复习试卷

一、奔驰模型

1. (2024九上·自贡开学考) 如图，P为等边三角形ABC内的一点，且P到三个顶点A ， B ， C的距离分别为3，4，5，则△ABC的面积为（　　）

A . $\text{[math]}$
B . $\text{[math]}$
C . $\text{[math]}$
D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九上·广州月考) 如图， $\text{[math]}$ 是正 $\text{[math]}$ 内一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，将线段BO以点 $\text{[math]}$ 为旋转中心逆时针旋转 $\text{[math]}$ 得到线段 $\text{[math]}$ ，下列结论，① $\text{[math]}$ 可以由 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得到；②点 $\text{[math]}$ 与 $\text{[math]}$ 的距离为5；③ $\text{[math]}$ ；④四边形 $\text{[math]}$ 面积 $\text{[math]}$ ；⑤ $\text{[math]}$ ，其中正确的结论是（）

A . ①④⑤ B . ①③④ C . ①③④⑤ D . ①③⑤

答案解析收藏纠错 + 选题
3. (2023九上·洪山月考) 如图，点D是等边△ABC内部的一点，∠ADC＝120°，AB²＝19， $\text{[math]}$ ，则线段BD的长度是．

答案解析收藏纠错 + 选题
4. (2023九上·上杭期中) 如图，在等边三角形 $\text{[math]}$ 内有一点 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
2. （2）若等边三角形边长为 $\text{[math]}$ ，求 $\text{[math]}$ 的最小值；
3. （3）如图，在正方形 $\text{[math]}$ 内有一点 $\text{[math]}$ ，且 $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ ，求正方形 $\text{[math]}$ 的边长．
答案解析收藏纠错 + 选题
5. (2024九上·邻水期末) 如图1，P为正方形 $\text{[math]}$ 内一点， $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
小明同学的想法是：不妨设 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，设法把 $\text{[math]}$ 相对集中，于是他将 $\text{[math]}$ 绕点B顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ （如图2），然后连接 $\text{[math]}$ ，问题得以解决．
1. （1）求出图2中 $\text{[math]}$ 的度数；
2. （2）请你参考小明同学的方法，解答下列问题：
  如图3，P是等边三角形 $\text{[math]}$ 内一点， $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
6. (2024九上·武昌月考) 【问题背景】：如图1，点 $\text{[math]}$ 是等边 $\text{[math]}$ 内一点，连接 $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，观察发现： $\text{[math]}$ 与 $\text{[math]}$ 的数量关系为________，直线 $\text{[math]}$ 与 $\text{[math]}$ 所夹的锐角为________度；
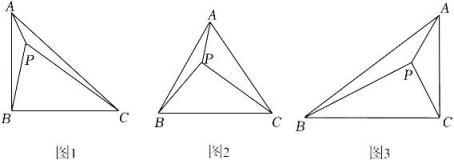
【尝试应用】：如图2，在等腰直角 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是等腰直角 $\text{[math]}$ 内一点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 面积；

【拓展创新】：如图3，在等腰 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 为平面内一点，且 $\text{[math]}$ ，直接写 $\text{[math]}$ 的值为________．

答案解析收藏纠错 + 选题
7. (2023九上·前郭尔罗斯期中) 阅读下面材料，并解决问题：
1. （1）如图①，在等边 $\text{[math]}$ 内有一点 $\text{[math]}$ ，若点 $\text{[math]}$ 到顶点 $\text{[math]}$ 的距离分别为 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；为了解决本题，我们可以将 $\text{[math]}$ 绕顶点 $\text{[math]}$ 旋转到 $\text{[math]}$ 处，此时 $\text{[math]}$ ，这样就可以利用旋转变换，将三条线段 $\text{[math]}$ 转化到一个三角形中，从而求出 $\text{[math]}$ 的度数，请你按照这个思路写出求解过程；
  图①
2. （2）能力提升
  如图②，在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 内一点，连接 $\text{[math]}$ ，且 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的值．
  图②
答案解析收藏纠错 + 选题
8. (2023九上·吉林期中) 阅读下面材料，并解决问题：
1. （1）如图①，在等边△ABC内有一点P ，若点P到顶点A、B、C的距离分别为3、4、5，求∠APB的度数；为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP'处，此时△ACP'≌△ABP，这样就可以利用旋转变换，将三条线段PA、PB、PC转化到一个三角形中，从而求出∠APB的度数，请你按照这个思路写出求解过程；
2. （2）能力提升
  如图②，在Rt△ABC中，∠ACB=90°，AC=1，∠ABC=30°，点O为Rt△ABC内一点，连接AO、BO、CO，且∠AOC=∠COB=∠BOA=120°，直接写出OA+OB+OC的值．
答案解析收藏纠错 + 选题
9. (2023九上·吉州月考) 问题解决
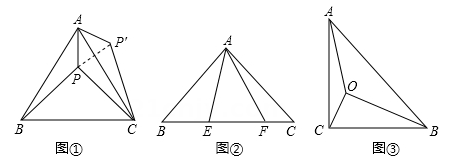
一节数学课上，老师提出了这样一个问题：如图①，点P是等边 $\text{[math]}$ 内的一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .你能求出 $\text{[math]}$ 的度数和等边 $\text{[math]}$ 的面积吗?小明通过观察、分析、思考，形成了如下思路：
如图①将 $\text{[math]}$ 绕点B逆时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，可得 $\text{[math]}$ 是等边三角形，根据勾股定理逆定理可得 $\text{[math]}$ 是直角三角形，从而使问题得到解决.
1. （1）结合小明的思路完成填空： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
2. （2）类比探究
  ①.如图②，若点P是正方形 $\text{[math]}$ 内一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数和正方形的面积.
  ②.如图③，若点P是正方形 $\text{[math]}$ 外一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数和正方形的面积.
答案解析收藏纠错 + 选题
10. (2023九上·东港月考) 阅读下面材料，并解决问题：
1. （1）如图 $\text{[math]}$ 等边 $\text{[math]}$ 内有一点 $\text{[math]}$ ，若点 $\text{[math]}$ 到顶点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的距离分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
  
  为了解决本题，我们可以将 $\text{[math]}$ 绕顶点 $\text{[math]}$ 旋转到 $\text{[math]}$ 处，此时 $\text{[math]}$ ≌ $\text{[math]}$ ，这样就可以利用旋转变换，将三条线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 转化到一个三角形中，从而求出 $\text{[math]}$ ；
2. （2）基本运用
  请你利用第 $\text{[math]}$ 题的解答思想方法，解答下面问题：
  如图 $\text{[math]}$ ， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 为 $\text{[math]}$ 上的点且 $\text{[math]}$ ，求证： $\text{[math]}$ ；
3. （3）能力提升
  如图 $\text{[math]}$ ，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 内一点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
11. (2023九上·大余月考) 回答下列问题：
1. （1）如图1，AB＝BC，当∠ABC＝90°时，将△PAB绕B点顺时针旋转90°，画出旋转后的图形．
2. （2）在（1）中，若PA＝2，PB＝4，PC＝6，求∠APB的大小．
3. （3）如图2，∠ABC＝60°，AB＝BC，且PA＝3，PB＝4，PC＝5，则△APC面积是．
4. （4）如图3，△ABC中，∠BAC＝60°，AB＝2AC，点P在△ABC内，且PA＝ $\text{[math]}$ ， PB＝5，PC＝2，求△ABC的面积．
答案解析收藏纠错 + 选题
12. (2021九上·交口期末) 阅读下面材料：
张明同学遇到这样一个问题：如图1，在正三角形ABC内有一点P，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
张明同学是这样思考的：如图2，利用旋转和全等的知识构造 $\text{[math]}$ ，连接 $\text{[math]}$ ，得到两个特殊的三角形，从而将问题解决．
1. （1）请你计算图1中 $\text{[math]}$ 的度数；
2. （2）参考张明同学思考问题的方法，解决下列问题：如图3，在正方形 $\text{[math]}$ 内有一点 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题

二、费马点模型

13. (2023九上·杭州期中) 如图，已知 $\text{[math]}$ ， AB=4，AC=6，点P在 $\text{[math]}$ 内，将 $\text{[math]}$ 绕着点A逆时针方向旋转60°得到 $\text{[math]}$ .则AE+PB+PC的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2024九上·武汉月考) 如图， $\text{[math]}$ 中， $\text{[math]}$ ，点P为 $\text{[math]}$ 内一点， $\text{[math]}$ ， $\text{[math]}$ ．若 $\text{[math]}$ ，且 $\text{[math]}$ 的长度不小于4，则 $\text{[math]}$ 长度的最小值为（）

A . 6 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2022九上·自流井期末) 如图，矩形ABCD中， $\text{[math]}$ ， BC＝3，P为矩形内一点，连接PA，PB，PC，则PA＋PB＋PC的最小值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2024九上·深圳开学考) 如图，矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是矩形内一个动点，且满足 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 内一个点，则 $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题
17. (2023九上·阳新期中) 如图，已知Rt△ABC中，∠ABC＝90°，∠ACB＝30°，斜边AC＝4，点P是三角形内的一动点，则PA+PB+PC的最小值是．

答案解析收藏纠错 + 选题
18. (2023九上·抚远期中) 如图，P是边长为2cm的正方形ABCD内一点，Q为边BC上一点，连接PA、PD、PQ，则PA+PD+PQ的最小值是

答案解析收藏纠错 + 选题
19. (2024九下·武昌模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，在 $\text{[math]}$ 内有一点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 的最小值为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
20. (2023九上·蓬江月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 内部一点，则点 $\text{[math]}$ 到 $\text{[math]}$ 三个顶点之和的最小值是．

答案解析收藏纠错 + 选题
21. (2020九上·路桥期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点P为 $\text{[math]}$ 内一点，连接PA，PB，PC，求PA+PB+PC的最小值，小华的解题思路，以点A为旋转中心，将 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，那么就将求PA+PB+PC的值转化为求PM+MN+PC的值，连接CN，当点P，M落在CN上时，此题可解.
1. （1）请判断 $\text{[math]}$ 的形状，并说明理由；
2. （2）请你参考小华的解题思路，证明PA+PB+PC=PM+MN+PC；
3. （3）当 $\text{[math]}$ ，求PA+PB+PC的最小值.
答案解析收藏纠错 + 选题
22. (2024九上·广州期末) 阅读下面材料，并解决问题：
1. （1）如图①等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求∠APB的度数．
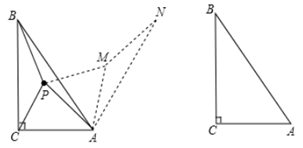
  为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP^'处，此时△ACP^'≌△ABP，这样就可以利用旋转变换，将三条线段PA、PB、PC转化到一个三角形中，从而求出∠APB＝ ▲ ；
2. （2）基本运用
  请你利用第（1）题的解答思想方法，解答下面问题
  已知如图②，△ABC中，∠CAB＝90°，AB＝AC，E、F为BC上的点且∠EAF＝45°，求证：EF²＝BE²+FC²；
3. （3）能力提升
  如图③，在Rt△ABC中，∠C＝90°，AC＝1，∠ABC＝30°，点O为Rt△ABC内一点，连接AO，BO，CO，且∠AOC＝∠COB＝∠BOA＝120°，求OA+OB+OC的值．
答案解析收藏纠错 + 选题