中考备考专题复习：多边形与平行四边形

更新时间：2017-02-08 浏览次数：1116 类型：二轮复习

一、单选题

1. 下列说法正确的是（）

A . 同位角相等 B . 过一点有且只有一条直线与已知直线平行 C . 过一点有且只有一条直线与已知直线垂直 D . 只用一种图形进行镶嵌，三角形、四边形、六边形都可以镶嵌

答案解析收藏纠错 + 选题
2. (2020九上·镇海期末) 下列正多边形中，绕其中心旋转72°后，能和自身重合的是（）

A . 正方形 B . 正五边形 C . 正六边形 D . 正八边形

答案解析收藏纠错 + 选题
3. 下列图形中，不能镶嵌成平面图案的是 ( )

A . 正三角形 B . 正四边形 C . 正五边形 D . 正六边形

答案解析收藏纠错 + 选题
4. 梯形ABCD中，AD∥BC，AB=CD=AD=2，∠B=60°，则下底BC的长是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5.
如图，在梯形ABCD中，AD//BC， ∠B=70°∠C=40°，DE//AB交BC于点E．若AD=3，BC=10，则CD的长是( )

A . 7 B . 10 C . 13 D . 14

答案解析收藏纠错 + 选题
6.
如图，AB∥CD∥EF，BC∥AD，AC为∠BAD的平分线，图中与∠AOE相等（不含∠AOE）的角有（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题
7. (2015九上·重庆期末) 正六边形的边心距为 $\text{[math]}$ ，这个正六边形的面积为（）

A . 2 $\text{[math]}$ B . 4 $\text{[math]}$ C . 6 $\text{[math]}$ D . 12

答案解析收藏纠错 + 选题
8. (2019八上·景县月考) 把边长相等的正五边形ABGHI和正六边形ABCDEF的AB边重合，按照如图的方式叠合在一起，连接EB，交HI于点K，则∠BKI的大小为（　　）

A . 90° B . 84° C . 72° D . 88°

答案解析收藏纠错 + 选题
9. (2023·荆州模拟)
如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若BF=6，AB=5，则AE的长为（　　）

A . 4 B . 6 C . 8 D . 10

答案解析收藏纠错 + 选题
10. (2020八上·南靖月考)
如图，在五边形ABCDE中，AB=AC=AD=AE，且AB∥ED，∠EAB=120°，则∠DCB=（　　）

A . 150° B . 160° C . 130° D . 60°

答案解析收藏纠错 + 选题
11. (2016·义乌) 小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（）

A . ①，② B . ①，④ C . ③，④ D . ②，③

答案解析收藏纠错 + 选题
12.
如图，在平面直角坐标系中，以O（0，0）、A（1，-1）、B（2，0）为顶点，构造平行四边形，下列各点中不能作为平行四边形第四个顶点坐标的是（　　　）

A . （3，-1） B . （-1，-1） C . （1，1） D . （-2，-1）

答案解析收藏纠错 + 选题

二、填空题

13. 正多边形的一个外角是72°，则这个多边形的内角和的度数是．

答案解析收藏纠错 + 选题
14. (2015九上·丛台期末) 现有一个正六边形的纸片，该纸片的边长为20cm，张萌想用一张圆形纸片将该正六边形纸片完全覆盖住，则圆形纸片的直径不能小于 cm．

答案解析收藏纠错 + 选题
15.
如图，已知四边形ABCD中，∠C=72°，∠D=81°．沿EF折叠四边形，使点A、B分别落在四边形内部的点A′、B′处，则∠1+∠2=°．

答案解析收藏纠错 + 选题
16.
如图，平行四边形ABCD绕点A逆时针旋转30°，得到平行四边形AB′C′D′（点B′与点B是对应点，点C′与点C是对应点，点D′与点D是对应点），点B′恰好落在BC边上，则∠C=

答案解析收藏纠错 + 选题
17. (2020八下·漯河期中)
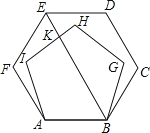
如图，在图（1）中，A₁、B₁、C₁分别是△ABC的边BC、CA、AB的中点，在图（2）中，A₂、B₂、C₂分别是△A₁B₁C₁的边B₁C₁、C₁A₁、A₁B₁的中点，…，按此规律，则第n个图形中平行四边形的个数共有个

答案解析收藏纠错 + 选题

三、综合题

18.
如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．
1. （1）试说明AC=EF；
2. （2）求证：四边形ADFE是平行四边形.
答案解析收藏纠错 + 选题
19. (2019·潍坊模拟)
如图，已知抛物线y=﹣ $\text{[math]}$ x²﹣ $\text{[math]}$ x+2与x轴交于A、B两点，与y轴交于点C
1. （1）求点A，B，C的坐标；
2. （2）点E是此抛物线上的点，点F是其对称轴上的点，求以A，B，E，F为顶点的平行四边形的面积；
3. （3）此抛物线的对称轴上是否存在点M，使得△ACM是等腰三角形？若存在，请求出点M的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
20. (2016·安徽)
如图1，A，B分别在射线OA，ON上，且∠MON为钝角，现以线段OA，OB为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP，△OBQ，点C，D，E分别是OA，OB，AB的中点．
1. （1）求证：△PCE≌△EDQ；
2. （2）延长PC，QD交于点R．
  ①如图1，若∠MON=150°，求证：△ABR为等边三角形；
  ②如图3，若△ARB∽△PEQ，求∠MON大小和 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
21. (2022九下·达州月考)
如图，矩形ABCD中，点E为BC上一点，F为DE的中点，且∠BFC=90°．
1. （1）当E为BC中点时，求证：△BCF≌△DEC；
2. （2）当BE=2EC时，求 $\text{[math]}$ 的值；
3. （3）设CE=1，BE=n，作点C关于DE的对称点C′，连结FC′，AF，若点C′到AF的距离是 $\text{[math]}$ ，求n的值．
答案解析收藏纠错 + 选题
22. (2016·江西)
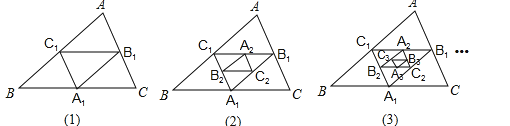
如图，将正n边形绕点A顺时针旋转60°后，发现旋转前后两图形有另一交点O，连接AO，我们称AO为“叠弦”；再将“叠弦”AO所在的直线绕点A逆时针旋转60°后，交旋转前的图形于点P，连接PO，我们称∠OAB为“叠弦角”，△AOP为“叠弦三角形”．
【探究证明】
1. （1）请在图1和图2中选择其中一个证明：“叠弦三角形”（△AOP）是等边三角形；
2. （2）如图2，求证：∠OAB=∠OAE′．
3. （3）图1、图2中的“叠弦角”的度数分别为，；
4. （4）图n中，“叠弦三角形”等边三角形（填“是”或“不是”）
5. （5）图n中，“叠弦角”的度数为（用含n的式子表示）
答案解析收藏纠错 + 选题