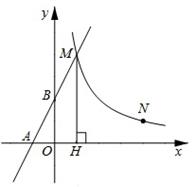
 B .
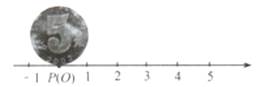
B . 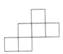


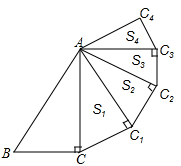
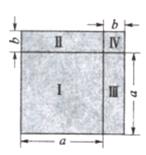
(a+b)2=(a+b)(a+b)
=a2+++b2
=a2++b2
|
组别(单位:分) |
频数 |
频率 |
|
50.5~60.5 |
20 |
0.1 |
|
60.5~70.5 |
40 |
0.2 |
|
70.5~80.5 |
70 |
b |
|
80.5~90.5 |
a |
0.3 |
|
90.5~100.5 |
10 |
0.05 |

请根据图表信息回答下列问题:
1=12
1+3=4=22:
1+3+5=9=32:
1+3+5+7=16=42:
1+3+5+…+(2n-1)=.(n是正整数)
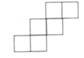
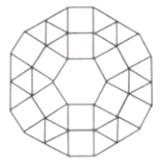
①第3层中分别含有 ▲ 块正方形和 ▲ 块正三角形地板砖:
②第n层中含有 ▲ 块正三角形地板砖(用含n的代数式表示)。
【应用】
该市打算在一个新建广场中央,采用图样式的图案铺设地面,现有1块正六边形、150块正方形和420块正三角形地板砖,问:铺设这样的图案,最多能铺多少层?请说明理由.
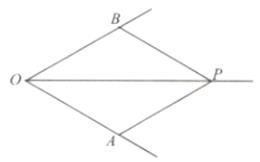
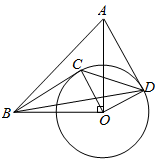
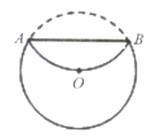
①求证:BC是⊙O的切线;
②求点C到OB的距离。