某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
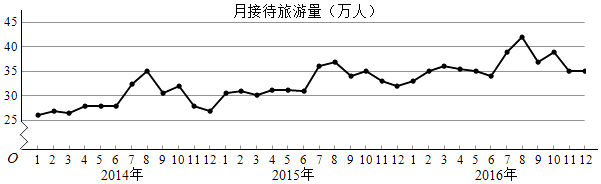
根据该折线图,下列结论错误的是( )
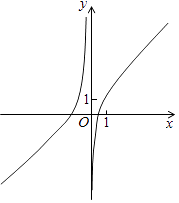 B .
B . 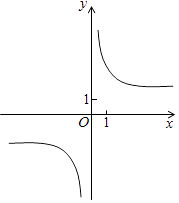 C .
C . 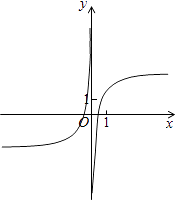 D .
D . 
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
如图四面体ABCD中,△ABC是正三角形,AD=CD.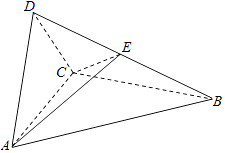
在直角坐标系xOy中,直线l1的参数方程为 ,(t为参数),直线l2的参数方程为
,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.