辽宁省大连市西岗区2019届数学中考模拟试卷（3月）

更新时间：2019-08-31 浏览次数：474 类型：中考模拟

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. 若关于x的一元二次方程(a+1)x²+x+a²﹣1＝0的一个根是0，则a的值为（）

A . 1 B . ﹣1 C . ±1 D . 0

答案解析收藏纠错 + 选题
3. 二次函数y＝﹣(x﹣1)²+3图象的对称轴是（）

A . .直线x＝1 B . 直线x＝﹣1 C . 直线x＝3 D . 直线x＝﹣3

答案解析收藏纠错 + 选题
4. 在Rt△ABC中∠C＝90°，∠A，∠B，∠C的对边分别为a、b、c，c＝3a，tanA的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
5. 在△ABC中，点D，E分别在AB，AC上，如果AD＝2，BD＝3，那么由下列条件能够判定DE∥BC的是（）

A . $\text{[math]}$ ＝ $\text{[math]}$ B . $\text{[math]}$ ＝ $\text{[math]}$ C . $\text{[math]}$ ＝ $\text{[math]}$ D . $\text{[math]}$ ＝ $\text{[math]}$

答案解析收藏纠错 + 选题
6. 如图，⊙O是△ABC的外接圆，∠OCB＝40°，则∠A的大小为（）

A . 40° B . 50° .80° D.100°

答案解析收藏纠错 + 选题
7. (2015七下·无锡期中) 如图，若干个全等的正五边形排成环状，图中所示的是前3个正五边形，要完成这一圆环还需正五边形的个数为（）

A . 10 B . 9 C . 8 D . 7

答案解析收藏纠错 + 选题
8. 给出下列命题：①圆既是轴对称图形，又是中心对称图形；②垂直于弦的直径平分这条弦；③在同圆或等圆中，相等的圆心角所对的弧相等，其中真命题是（）

A . ①② B . ②③ C . ①③ D . ①②③

答案解析收藏纠错 + 选题

二、填空题

9. 方程（x﹣1）（x+2）=0的解是．

答案解析收藏纠错 + 选题
10. 一根1.5米长的标杆直立在水平地面上，它在阳光下的影长为2.1米，此时标杆旁边一棵杨树的影长为10.5米，则这棵杨树高为米.

答案解析收藏纠错 + 选题
11. 如图，⊙O的半径为10cm，AB是⊙O的弦，OC⊥AB于D，交⊙O于点C，且CD＝4cm，弦AB的长为cm.

答案解析收藏纠错 + 选题
12. (2019八上·昭通期末) 已知圆锥的底面半径为3，母线长为6，则此圆锥侧面展开图的圆心角是．

答案解析收藏纠错 + 选题
13. 商店里某套衣服原本售价为400元每套，经过连续两次降价后，现价为每套256元，假设两次降价的百分率都为x，根据题意可列方程为.

答案解析收藏纠错 + 选题
14. 抛物线 $\text{[math]}$ 经过原点，那么该抛物线在对称轴左侧的部分是的.（填“上升”或“下降”）

答案解析收藏纠错 + 选题
15. 如图，在△ABC中，AD是高，BD＝6，CD＝4，tan∠BAD＝ $\text{[math]}$ ，P是线段AD上一动点，一机器人从点A出发沿AD以 $\text{[math]}$ 个单位/秒的速度走到P点，然后以1个单位/秒的速度沿PC走到C点，共用了t秒，则t的最小值为.

答案解析收藏纠错 + 选题
16. 如图，直线a与直线b相交于点A，与直线c交于点B，∠l=120°，∠2=45°.若将直线b绕点A逆时针旋转一定角度，使直线b与直线c平行，则这个旋转角至少是°

答案解析收藏纠错 + 选题

三、解答题

17.
1. （1）计算： $\text{[math]}$ .
2. （2）解方程：3x²﹣4x﹣1＝0.
答案解析收藏纠错 + 选题
18. 如图，已知四边形ABCD是平行四边形，P为DC延长线上一点，AP分别交BD，BC于点M，N.
1. （1）图中相似三角形共有对；
2. （2）证明：AM²＝MN•MP；
3. （3）若AD＝6，DC：CP＝2：1，求BN的长.
答案解析收藏纠错 + 选题
19. 如图，一次函数y₁＝x﹣ $\text{[math]}$ 与x轴交点A恰好是二次函数y₂与x轴的其中一个交点，已知二次函数图象的对称轴为x＝1，并与y轴的交点为D(0，1).
1. （1）求二次函数的解析式；
2. （2）设该二次函数与一次函数的另一个交点为C点，连接DC，求三角形ADC的面积.
3. （3）根据图象，直接写出当y₁＞y₂时x的取值范围.
答案解析收藏纠错 + 选题
20. 某网店准备经销一款儿童玩具，每个进价为35元，经市场预测，包邮单价定为50元时，每周可售出200个，包邮单价每增加1元销售将减少10个，已知每成交一个，店主要承付5元的快递费用，设该店主包邮单价定为x(元)(x＞50)，每周获得的利润为y(元).
1. （1）求该店主包邮单价定为53元时每周获得的利润；
2. （2）求y与x之间的函数关系式；
3. （3）该店主包邮单价定为多少元时，每周获得的利润最大？最大值是多少？
答案解析收藏纠错 + 选题
21. 在平面直角坐标系中，△ABC的位置如图所示.(每个小方格都是边长为1个单位长度的正方形)
1. （1）画出△ABC关于原点对称的△A'B'C'；
2. （2）将△A'B'C'绕点C'顺时针旋转90°，画出旋转后得到的△A″B″C″，并直接写出此过程中线段C'A'扫过图形的面积.(结果保留π)
答案解析收藏纠错 + 选题
22. 某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．
1. （1）求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式；
2. （2）求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？
3. （3）如果该企业要使每天的销售利润不低于4000元，那么销售单价应控制在什么范围内？
答案解析收藏纠错 + 选题
23. 如图，正方形ABCD的边长为4，E是BC边的中点，点P在射线AD上，过P作PF⊥AE于F，设PA＝x.
1. （1）求证：△PFA∽△ABE；
2. （2）若以P，F，E为顶点的三角形也与△ABE相似，试求x的值；
3. （3）试求当x取何值时，以D为圆心，DP为半径的⊙D与线段AE只有一个公共点.
答案解析收藏纠错 + 选题
24. 在数学活动课上，老师提出了一个问题：把一副三角尺如图1摆放，直角三角尺的两条直角边分别垂直或平行，60°角的顶点在另一个三角尺的斜边上移动，在这个运动过程中，有哪些变量，能研究它们之间的关系吗？
小林选择了其中一对变量，根据学习函数的经验，对它们之间的关系进行了探究.下面是小林的探究过程，请补充完整：
1. （1）画出几何图形，明确条件和探究对象；
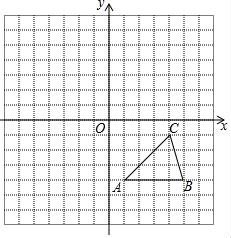
  如图2，在Rt△ABC中，∠C＝90°，AC＝BC＝6cm，D是线段AB上一动点，射线DE⊥BC于点E，∠EDF＝°，射线DF与射线AC交于点F.设B，E两点间的距离为xcm，E，F两点间的距离为ycm.
2. （2）通过取点、画图、测量，得到了x与y的几组值，如下表：
  
  x/cm
  
  0
  
  1
  
  2
  
  3
  
  4
  
  5
  
  6
  
  y/cm
  
  6.9
  
  5.3
  
  4.0
  
  3.3
  
  4.5
  
  6
  
  (说明：补全表格时相关数据保留一位小数)
3. （3）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
4. （4）结合画出的函数图象，解决问题：当△DEF为等边三角形时，BE的长度约为cm.
答案解析收藏纠错 + 选题
25. 如图，在△ABC中，∠BAC＝90°，AB＝AC，点D是BC上一动点，连接AD，过点A作AE⊥AD，并且始终保持AE＝AD，连接CE.
1. （1）求证：△ABD≌△ACE；
2. （2）若AF平分∠DAE交BC于F，探究线段BD，DF，FC之间的数量关系，并证明；
3. （3）在(2)的条件下，若BD＝3，CF＝4，求AD的长.
答案解析收藏纠错 + 选题
26. 如图1，在平面直角坐标系中，抛物线y＝﹣ $\text{[math]}$ x²+2 $\text{[math]}$ x﹣ $\text{[math]}$ 与x轴交于A、B两点(点A在点B的左侧)，与y轴交于点C，顶点为D，对称轴与x轴交于点E，直线CE交抛物线于点F(异于点C)，直线CD交x轴交于点G.
1. （1）如图1，求直线CE的解析式和顶点D的坐标；
2. （2）如图1，点P为直线CF上方抛物线上一点，连接PC、PF，当△PCF的面积最大时，点M是过P垂直于x轴的直线l上一点，点N是抛物线对称轴上一点，求FM+MN+NO的最小值；
3. （3）如图2，过点D作DI⊥DG交x轴于点I，将△GDI沿射线GB方向平移至△G′D′I′处，将△G′D′I′绕点D′逆时针旋转α(0＜α＜180°)，当旋转到一定度数时，点G′会与点I重合，记旋转过程中的△G′D′I′为△G″D′I″，若在整个旋转过程中，直线G″I″分别交x轴和直线GD′于点K、L两点，是否存在这样的K、L，使△GKL为以∠LGK为底角的等腰三角形？若存在，求此时GL的长.
答案解析收藏纠错 + 选题