(3)
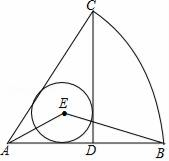
如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在

、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).

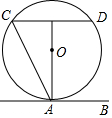


的一个根吗?为什么?
的值.

