 B .
B .  C .
C .  D .
D . 





|
入住的房间数量 |
房间价格 |
总维护费用 |
|
|
提价前 |
60 |
200 |
60×20 |
|
提价后 |
|
|
|

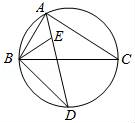
特例感知:

①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD=BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为.
猜想论证:
