江西省宜春市2019年中考数学4月模拟考试试卷

更新时间：2020-05-13 浏览次数：190 类型：中考模拟

一、单选题

1. (2024九下·太平模拟) $\text{[math]}$ 的相反数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021七下·汉台期末) 目前，世界上能制造出的最小晶体管的长度只有0.00000004m，将0.00000004用科学记数法表示为（）

A . 0.4×10⁸ B . 4×10⁸ C . 4×10^﹣⁸ D . ﹣4×10⁸

答案解析收藏纠错 + 选题
3. (2022九下·北京市开学考) 下列图形中，是中心对称图形但不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2019·宜春模拟) 已知一元二次方程x²+x﹣1=0，下列判断正确是（）

A . 该方程有两个相等的实数根 B . 该方程有一个根为1 C . 该方程没有实数根 D . 该方程有一个根为负数

答案解析收藏纠错 + 选题
5. (2019七下·青岛期末) 如图，在△ABC中，AC＝BC，有一动点P从点A出发，沿A→C→B→A匀速运动，则CP的长度s与时间t之间的函数关系用图象描述大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2023八下·自贡月考) 如图，正方形ABCD中，E为AB中点，FE⊥AB，AF=2AE，FC交BD于O，则∠DOC的度数为（）

A . 60° B . 67.5° C . 75° D . 54°

答案解析收藏纠错 + 选题

二、填空题

7. (2019·宜春模拟) 分解因式：3x²﹣9=．

答案解析收藏纠错 + 选题
8. (2019·宜春模拟) 数据1，0，5，3，5，π，4的中位数是．

答案解析收藏纠错 + 选题
9. (2019·宜春模拟) 从某一个方向观察一个正六棱柱，可看到如图所示的图形，其中四边形ABCD为矩形，E、F分别是AB、DC的中点，若AD=8，AB=6，则这个正六棱柱的侧面积为．

答案解析收藏纠错 + 选题
10. (2019·宜春模拟) 不等式组 $\text{[math]}$ 的整数解为．

答案解析收藏纠错 + 选题
11. (2019·宜春模拟) 已知如图，矩形OCBD如图所示，OD=2，OC=3，反比例函数的图象经过点B，点A为第一象限双曲线上的动点（点A的横坐标大于2），过点A作AF⊥BD于点F，AE⊥x轴于点E，连接OB，AD，若△OBD∽△DAE，则点A的坐标是．

答案解析收藏纠错 + 选题
12. (2020·本溪模拟) 如图，Rt△ABC纸片中，∠C=90°，AC=6，BC=8，点D在边BC 上，以AD为折痕将△ABD折叠得到△AB′D，AB′与边BC交于点E．若△DEB′为直角三角形，则BD的长是．

答案解析收藏纠错 + 选题

三、解答题

13. (2019·宜春模拟)
1. （1）解方程： $\text{[math]}$ ；
2. （2）如图，四边形ABCD的对角线AC、BD交于点O，已知O是AC的中点，AE=CF，DE∥BE，求证：△BOE≌△DOF．
答案解析收藏纠错 + 选题
14. (2020·定远模拟) 我市某校组织爱心捐书活动，准备将一批捐赠的书打包寄往贫困地区，其中每包书的数目相等．第一次他们领来这批书的 $\text{[math]}$ ，结果打了16个包还多40本；第二次他们把剩下的书全部取来，连同第一次打包剩下的书一起，刚好又打了9个包，那么这批书共有多少本？

答案解析收藏纠错 + 选题
15. (2020九上·邯郸月考) 为落实“垃圾分类”，环保部门要求垃圾要按A，B，C，D四类分别装袋、投放，其中A类指废电池，过期药品等有毒垃圾，B类指剩余食品等厨余垃圾，C类指塑料、废纸等可回收物，D类指出其他垃圾，小明、小亮各投放了一袋垃圾．
1. （1）直接写出小明投放的垃圾恰好是A类的概率；
2. （2）求小亮投放的垃圾与小明投放的垃圾是同一类的概率．
答案解析收藏纠错 + 选题
16. (2019·宜春模拟) 如图，下列正方形网格的每个小正方形的边长均为1，⊙O的半径为 $\text{[math]}$ ，规定：顶点既在圆上又是正方形格点的直角三角形称为“圆格三角形”，请按下列要求使用无刻度的直尺各画一个“圆格三角形”，
1. （1）一个锐角的正切值为 $\text{[math]}$
2. （2）面积为8
答案解析收藏纠错 + 选题
17. (2019·宜春模拟) 如图，已知平行四边形OBDC的对角线相交于点E，其中O（0，0），B（3，4），C（m，0），反比例函数y= $\text{[math]}$ （k≠0）的图象经过点B．
1. （1）求反比例函数的解析式；
2. （2）若点E恰好落在反比例函数y= $\text{[math]}$ 上，求平行四边形OBDC的面积．
答案解析收藏纠错 + 选题
18. (2019·宜春模拟) 某中学现有学生2650人，学校为了进一步了解学生课余生活，组织调查各兴趣小组活动情况，为此校学生会进行了一次随机抽样调查，根据采集到的数据，绘制如下两个统计图（不完整）

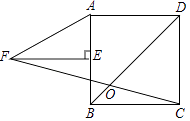
请你根据两个统计图中提供的信息，解答下列问题：
1. （1）这次抽样调查的样本容量是多少？在图2中，请将条形统计图中的“体育”部分的图形补充完整；
2. （2）爱好“书画”的人数占被调查人数的百分数是多少？估计该中学现有的学生中，爱好“书画”的人数；
3. （3）求爱好“音乐”的人数对应扇形圆心角的度数．
答案解析收藏纠错 + 选题
19. (2019·宜春模拟) 一书架上的方格中放置四本厚度和长度相同的书，其中书架方格长BF=40cm，书的长度AB=20cm，设一本书的厚度为xcm．
1. （1）如图1左边三本书紧贴书架方格内侧竖放，右边一本书自然向左斜放，支撑点为C，E，最右侧书一个角正好靠在方格内侧上，若CG=4cm，求EF的长度；
2. （2）如图2左边两本书紧贴书架方格内侧竖放，右边两本书自然向左斜放，支撑点为C，E，最右侧书的下面两个角正好靠在方格内上，若∠DCE=30°，求x的值（保留一位小数）．（参考数据： $\text{[math]}$ =1.414， $\text{[math]}$ =1.732）
答案解析收藏纠错 + 选题
20. (2019·宜春模拟) 如图1，点E为正方形ABCD的边AB上一点，EF⊥EC，且EF=EC，连接AF．
1. （1）求∠EAF的度数；
2. （2）如图2，连接FC交BD于M，交AD于N．求证：BD=AF+2DM．
答案解析收藏纠错 + 选题
21. (2020·湖州模拟) 如图，⊙A过▱OBCD的三顶点O、D、C，边OB与⊙A相切于点O，边BC与⊙O相交于点H，射线OA交边CD于点E，交⊙A于点F，点P在射线OA上，且∠PCD=2∠DOF，以O为原点，OP所在的直线为x轴建立平面直角坐标系，点B的坐标为（0，﹣2）．
1. （1）若∠BOH=30°，求点H的坐标；
2. （2）求证：直线PC是⊙A的切线；
3. （3）若OD= $\text{[math]}$ ，求⊙A的半径．
答案解析收藏纠错 + 选题
22. (2019·宜春模拟) 在四边形ABCD中，点E为AB边上的一点，点F为对角线BD上的一点，且EF⊥AB．
1. （1）若四边形ABCD为正方形．
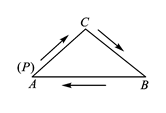
  如图1，请直接写出AE与DF的数量关系；
2. （2）将△EBF绕点B逆时针旋转到图2所示的位置，连接AE，DF，猜想AE与DF的数量关系并说明理由．
3. （3）若四边形ABCD为矩形，BC=mAB，其他条件都不变．
  ①如图3，猜想AE与DF的数量关系并说明理由；
  
  ②将△EBF绕点B顺时针旋转α（0°＜α＜90°）得到△E′BF′，连接AE′，DF′，请在图4中画出草图，并直接写出AE′和DF′的数量关系．
答案解析收藏纠错 + 选题
23. (2019·宜春模拟) 如图，抛物线y=ax²+2x与x轴相交于点B，其对称轴为x=3．
1. （1）求直线AB的解析式；
2. （2）过点O作直线l，使l∥AB，点P是l上一动点，设以点A、B、O、P为顶点的四边形面积为S，点P的横坐标为t，当0＜S≤18时，求t的取值范围；
3. （3）在（2）的条件下，当t取最大值时，抛物线上是否存在点Q，使△OPQ为直角三角形且OP为直角边，若存在，求出点Q的坐标；若不存在，说明理由．
答案解析收藏纠错 + 选题