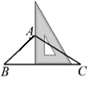
 B .
B . 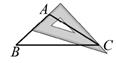 C .
C . 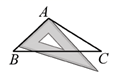 D .
D . 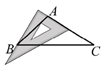
 B .
B .  C .
C .  D .
D . 
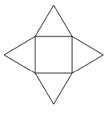
下列推断错误的是( )
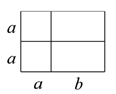
译文:现有一根杆和一条绳索,用绳索去量杄,绳索比杆子长5尺;如果将绳索对折后再去量竿,就比竿子短5尺,问绳索长几尺?注:一托 尺
设绳索长X尺,竿子长y尺,依题意,可列方程组为.
①对于任意四边形 ,四边形
都是平行四边形;
②若四边形 是平行四边形,则
与
交于点O;
③若四边形 是矩形,则四边形
也是矩形;
④若四边形 是正方形,则四边形
也一定是正方形.
所有符合题意推断的序号是.

小聪根据学习函数的经验,利用上述表格所反映出的 与x之间的变化规律,分别对函数
的图象与性质进行了探究.
下面是小聪的探究过程,请补充完整:
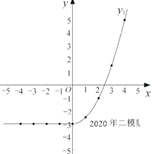
①当 时,对应的函数值
约为;
②写出函数 的一条性质:;
③当 时,
的取值范围是.
a.八年级学生成绩的频数分布直方图如下(数据分为五组: )
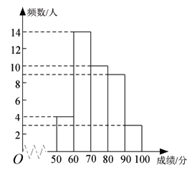
b.八年级学生成绩在 这一组的是:
70 71 73 73 73 74 76 77 78 79
c.九年级学生成绩的平均数、中位数、众数、优秀率如下:
| 平均数 | 中位数 | 众数 | 优秀率 |
| 79 | 76 | 84 | 40% |
根据以上信息,回答下列问题:
①预估九年级学生达到优秀的约有人;
②如果年级排名在前70名的学生可以被评选为“运动达人”,预估八年级学生至少要达到分才可以入选.
已知直线 与
轴交于点M,与y轴交于点
的半径为r.