 B .
B .  C .
C . 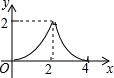 D .
D . 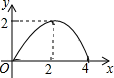
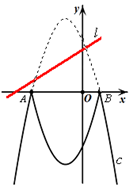
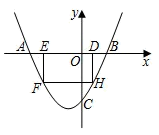
①如果存在两个实数p≠q,使得ap2+bp+c=aq2+bq+c,则 ②存在三个实数m≠n≠s,使得am2+bm+c=an2+bn+c=as2+bs+c③如果ac<0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c④如果ac>0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c


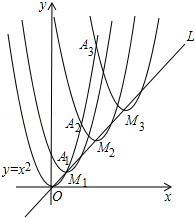
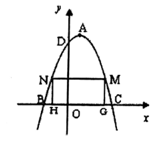
①抛物线的顶点M1 , M2 , M3 , …Mn , …都在直线L:y=x上;
②抛物线依次经过点A1 , A2 , A3…An , ….
则M2016顶点的坐标为.