B .
B .  D .
D . 
 B .
B .  C .
C . 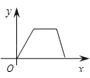 D .
D . 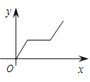
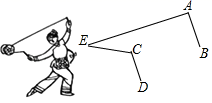
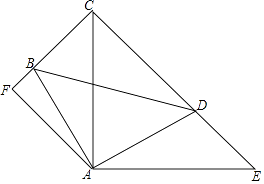
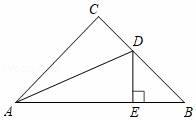
①AD平分∠CDE,
②∠BAC=∠BDE,
③DE平分∠ADB,
④BE+AC=AB,
其中正确的有( )

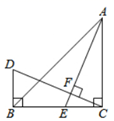
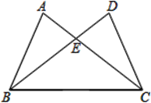


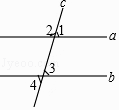
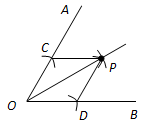
解:∵AD∥BE(已知),
∴∠A=∠ ▲ ( ▲ )
又∴∠1=∠2(已知),
∴AC∥ ▲ ( ▲ )
∴∠3=∠ ▲ ( ▲ )
∴∠A= ▲ ( ▲ )
|
鞋长x(cm) |
… |
22 |
23 |
24 |
25 |
26 |
… |
|
码数y(码) |
… |
34 |
36 |
38 |
40 |
42 |
… |
请你替小明解决下列问题:
①当鞋长为28cm时,鞋子的码数是多少?
②写出y与x之间的关系式;
③已知姚明的鞋子穿52码时,则他穿的鞋长是多长?
数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性,从而可以帮助我们快速解题.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如:利用图形的几何意义证明完全平方公式.
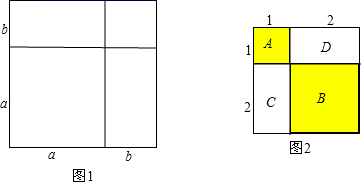
证明:将一个边长为a的正方形的边长增加b,形成两个矩形和两个正方形,如图1:
这个图形的面积可以表示成:
(a+b)2或a2+2ab+b2
∴(a+b)2 =a2+2ab+b2
这就验证了两数和的完全平方公式.
类比解决:
问题提出:如何利用图形几何意义的方法证明:13+23=32?
如图2,A表示1个1×1的正方形,即:1×1×1=13
B表示1个2×2的正方形,C与D恰好可以拼成1个2×2的正方形,因此:B、C、D就可以表示2个2×2的正方形,即:2×2×2=23而A、B、C、D恰好可以拼成一个(1+2)×(1+2)的大正方形.
由此可得:13+23=(1+2)2=32
请用上面的表示几何图形面积的方法探究:13+23+33+…+n3=.(直接写出结论即可,不必写出解题过程)