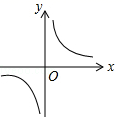
 B .
B . 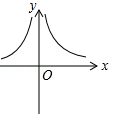 C .
C . 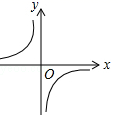 D .
D . 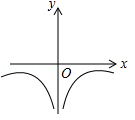
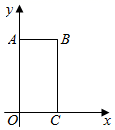

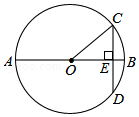

| 等级 | 频数 | 频率 |
| A | 4 | 0.08 |
| B | 20 | a |
| C | b | 0.3 |
| D | 11 | 0.22 |
请根据所给信息,解答下列问题:
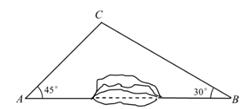
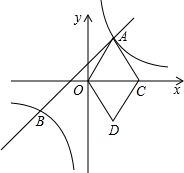
①点P在运动过程中,线段PD的长度是否存在最大值?若存在,请求出点D的坐标;若不存在,请说明理由;
②以P、D、C为顶点的三角形与△COA相似时,求出点P的坐标.