北京密云区2020年中考数学一模试卷

更新时间：2024-11-06 浏览次数：227 类型：中考模拟

一、单选题

1. (2021七上·舒兰期末) 下列四个角中，最有可能与70°角互补的角是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020七上·海勃湾期末) $\text{[math]}$ 是第五代移动通信技术， $\text{[math]}$ 网络理论下载速度可以达到每秒 $\text{[math]}$ 以上，这意味着下载一部高清电影只需1秒.将1300000用科学记数法表示应为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020·密云模拟) 下列各式计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021九下·西城月考) 下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2023七下·龙口期末) 实数 $\text{[math]}$ 在数轴上的对应点的位置如图所示，下列关系式不成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020·密云模拟) 如图，点A ， B是正方体上的两个顶点，将正方体按图中所示方式展开，则在展开图中B 点的位置为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020·密云模拟) 《九章算术》中记载：“今有上禾三秉，益实六斗，当下禾十秉.下禾五秉，益实一斗，当上禾二秉.问上、下禾实一秉各几何?”其大意是：今有上等稻子三捆，若打出来的谷子再加六斗，则相当于十捆下等稻子打出来的谷子.有下等稻子五捆，若打出来的谷子再加一斗，则相当于两捆上等稻子打出来的谷子.问上等、下等稻子每捆能打多少斗谷子?设上等稻子每捆能打x斗谷子，下等稻子每捆能打y斗谷子，根据题意，可列方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

8. (2020·密云模拟) 据统计表明，2019年中国电影总票房高达642.7亿元，其中动画电影发展优势逐渐显现出来．下面的统计表反映了六年来中国上映的动画电影的相关数据：

2014-2019年中国动画电影影片数量及票房统计表

年份	国产动画影片数量（单位：部）	国产动画影片票房（单位：亿元）	进口动画影片数量（单位：部）	进口动画影片票房（单位：亿元）
2014	21	11.4	18	19.5
2015	26	19.8	14	24.2
2016	24	13.8	24	57.0
2017	16	13.0	21	36.8
2018	21	15.8	22	25.0
2019	31	70.95	42	44.09

（以上数据摘自《中国电影产业市场前瞻与投资战略规划分析报告》）

根据上表数据得出以下推断，其中结论错误的是（）

A . 2017年至2019年，国产动画影片数量均低于进口动画影片数量 B . 2019年与2018年相比，中国动画电影的数量增加了50%以上 C . 2014年至2019年，中国动画电影的总票房逐年增加 D . 2019年，中国动画电影的总票房占中国电影总票房的比例不足20%

答案解析收藏纠错 + 选题

二、填空题

9. (2020·密云模拟) 请写出一个绝对值大于2的负无理数：．

答案解析收藏纠错 + 选题
10. (2022七下·鄞州期中) 若代数式 $\text{[math]}$ 有意义，则 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
11. (2020·密云模拟) 在如图所示的几何体中，其三视图中有三角形的是（填序号）．

答案解析收藏纠错 + 选题
12. (2024八上·乳山期末) 化简 $\text{[math]}$ 的结果是．

答案解析收藏纠错 + 选题
13. (2020·密云模拟) 如图， $\text{[math]}$ 为 $\text{[math]}$ 直径，点 $\text{[math]}$ 为 $\text{[math]}$ 上一点，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，且 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，若 $\text{[math]}$ 的半径为4， $\text{[math]}$ ，则弦 $\text{[math]}$ 的长度为．

答案解析收藏纠错 + 选题
14. (2020·密云模拟) 为做好疫情宣传巡查工作，各地积极借助科技手段加大防控力度．如图，亮亮在外出期间被无人机隔空喊话“戴上口罩，赶紧回家”．据测量，无人机与亮亮的水平距离是15米，当他抬头仰视无人机时，仰角恰好为 $\text{[math]}$ ，若亮亮身高1.70米，则无人机距离地面的高度约为米．（结果精确到0.1米，参考数据： $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题

15. (2020·密云模拟) 为提升英语听力及口语技能，小明打算在手机上安装一款英语口语APP辅助练习．他分别从甲、乙、丙三款口语APP中随机选取了1000条网络评价进行对比，统计如下：

等级评价数量 APP	五星	四星	三星	二星	一星	合计
甲	562	286	79	48	25	1000
乙	517	393	52	21	17	1000
丙	504	210	136	116	34	1000

（说明：网上对于口语APP的综合评价从高到低依次为五星、四星、三星、二星和一星）.

小明选择（填“甲”、“乙”或“丙”）款英语口语APP，能获得良好口语辅助练习（即评价不低于四星）的可能性最大．

答案解析收藏纠错 + 选题

16. (2020·密云模拟) 如图(1) ，将一个正六边形各边延长，构成一个正六角星形AFBDCE，它的面积为1，取△ABC和△DEF各边中点，连接成正六角星形A₁F₁B₁D₁C₁E₁ ，如图(2)中阴影部分；取△A₁B₁C₁和₁D₁E₁F₁各边中点，连接成正六角星形A₂F₂B₂D₂C₂E ₂F₂ ，如图(3) 中阴影部分；如此下去…，则正六角星形A_nF_nB_nD_nC_nE_nF_n的面积为.

答案解析收藏纠错 + 选题

三、解答题

17. (2021·岳池模拟) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2021八上·肇源期末) 解不等式组 $\text{[math]}$ ，并写出它的所有整数解．

答案解析收藏纠错 + 选题
19. (2021九下·西城月考) 下面是小菲设计的“作一个角等于已知角的二倍”的尺规作图过程．
已知： $\text{[math]}$ 中， $\text{[math]}$ ．

求作： $\text{[math]}$ ，使得 $\text{[math]}$ ．

作法：如图，

①分别以点 $\text{[math]}$ 和点 $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 的长为半径作弧，两弧交于 $\text{[math]}$ 、 $\text{[math]}$ 点，作直线 $\text{[math]}$ ；

②分别以点 $\text{[math]}$ 和点 $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 的长为半径作弧，两弧交于 $\text{[math]}$ 、 $\text{[math]}$ 点，作直线 $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 交于点 $\text{[math]}$ ；

③连接 $\text{[math]}$ 和 $\text{[math]}$ ；

④以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 的长为半径作 $\text{[math]}$ ．

所以 $\text{[math]}$ ．

根据小菲设计的尺规作图过程．
1. （1）使用直尺和圆规，补全图形（保留作图痕迹）；
2. （2）完成下面的证明．
  
  证明：连接 $\text{[math]}$
  
  ∵ $\text{[math]}$ 和 $\text{[math]}$ 分别为 $\text{[math]}$ 、 $\text{[math]}$ 的垂直平分线，
  
  ∴ $\text{[math]}$ ．
  
  ∴ $\text{[math]}$ 是 $\text{[math]}$ 的外接圆．
  
  ∵点 $\text{[math]}$ 是 $\text{[math]}$ 上的一点，
  
  ∴ $\text{[math]}$ ．（）．（填推理的依据）
答案解析收藏纠错 + 选题
20. (2022九上·连云月考) 已知，关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有两个不相等的实数根.
1. （1）求m的取值范围；
2. （2）如果m为非负整数，且该方程的根都是整数，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
21. (2020·密云模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ． $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是菱形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
22. (2020·密云模拟) 如图，在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 、 $\text{[math]}$ 的值；
2. （2）点 $\text{[math]}$ 是 $\text{[math]}$ 轴上的一点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线，交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，交反比例函数 $\text{[math]}$ 的图象于点 $\text{[math]}$ ．横、纵坐标都是整数的点叫做整点．记 $\text{[math]}$ 的图象在点 $\text{[math]}$ ， $\text{[math]}$ 之间的部分与线段 $\text{[math]}$ ， $\text{[math]}$ 围成的区域（不含边界）为 $\text{[math]}$ ．
  ①当 $\text{[math]}$ 时，直接写出区域 $\text{[math]}$ 内的整点的坐标为（）；
  
  ②若区域 $\text{[math]}$ 内恰有6个整点，结合函数图象，求出 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
23. (2020·密云模拟) 如图， $\text{[math]}$ 为 $\text{[math]}$ 的直径，点 $\text{[math]}$ 、点 $\text{[math]}$ 为 $\text{[math]}$ 上异于 $\text{[math]}$ 、 $\text{[math]}$ 的两点，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ 的半径为 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
24. (2020·密云模拟) 2020年新冠肺炎疫情发生以来，我市广大在职党员积极参与社区防疫工作，助力社区坚决打赢疫情防控阻击战．其中， $\text{[math]}$ 社区有500名在职党员，为了解本社区2月-3月期间在职党员参加应急执勤的情况， $\text{[math]}$ 社区针对执勤的次数随机抽取50名在职党员进行调查，并对数据进行了整理、描述和分析，下面给出了部分信息．

其中，应急执勤次数在 $\text{[math]}$ 这一组的数据是：

20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29

请根据所给信息，解答下列问题：
1. （1） $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）请补全频数分布直方图；
3. （3）随机抽取的50名在职党员参加应急执勤次数的中位数是；
4. （4）请估计2月-3月期间 $\text{[math]}$ 社区在职党员参加应急执勤的次数不低于30次的约有人．
答案解析收藏纠错 + 选题

25. (2020·密云模拟) 如图，点 $\text{[math]}$ 是线段 $\text{[math]}$ 的中点， $\text{[math]}$ 是以 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为直径的半圆弧，点 $\text{[math]}$ 是 $\text{[math]}$ 上一动点，过点 $\text{[math]}$ 作射线 $\text{[math]}$ 的垂线，垂足为 $\text{[math]}$ ．已知 $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ 、 $\text{[math]}$ 两点间的距离为 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 两点间的距离为 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 两点间的距离为 $\text{[math]}$ ．

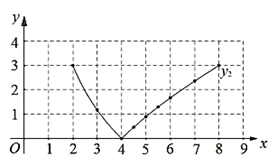
小丽根据学习函数的经验，分别对函数 $\text{[math]}$ 和 $\text{[math]}$ 随自变量 $\text{[math]}$ 变化而变化的规律进行了探究．下面是小丽的探究过程，请将它补充完整：

（1）按照下表中自变量 $\text{[math]}$ 的值进行取点、画图、测量，分别得到 $\text{[math]}$ 和 $\text{[math]}$ 与 $\text{[math]}$ 的几组对应值：

$\text{[math]}$	2	3	4	4.5	5	5.5	6	7	8
$\text{[math]}$	0	2.76	$\text{[math]}$	2.96	2.86	2.70	2.49	1.85	0
$\text{[math]}$	3.00	1.18	0	0.47	0.90	1.30	1.37	2.36	3.00

经测量，m的值是；（保留一位小数）

（2）在同一平面直角坐标系 $\text{[math]}$ 中，描出补全后的表中各组数值所对应的点 $\text{[math]}$ 和 $\text{[math]}$ ，并画出函数 $\text{[math]}$ 、 $\text{[math]}$ 的图象；
（3）结合函数图象，解决问题：连接 $\text{[math]}$ ，当 $\text{[math]}$ 是等腰三角形时， $\text{[math]}$ 的长度约为 $\text{[math]}$ ．（结果保留一位小数）

答案解析收藏纠错 + 选题

26. (2020·密云模拟) 在平面直角坐标系 $\text{[math]}$ 中，已知抛物线 $\text{[math]}$ ．
1. （1）抛物线的对称轴为；
2. （2）若当 $\text{[math]}$ 时， $\text{[math]}$ 的最小值是 $\text{[math]}$ ，求当 $\text{[math]}$ 时， $\text{[math]}$ 的最大值；
3. （3）已知直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 存在两个交点，设左侧的交点为点 $\text{[math]}$ ，当 $\text{[math]}$ 时，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
27. (2020·密云模拟) 已知 $\text{[math]}$ ，点 $\text{[math]}$ 在射线 $\text{[math]}$ 上，点 $\text{[math]}$ 是射线 $\text{[math]}$ 上的一个动点（不与点 $\text{[math]}$ 重合）．点 $\text{[math]}$ 关于 $\text{[math]}$ 的对称点为点 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ 和 $\text{[math]}$ ，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，且满足 $\text{[math]}$ ．小明在探究图形运动的过程中发现： $\text{[math]}$ 始终成立．
1. （1）如图1，当 $\text{[math]}$ 时；
  ①求证： $\text{[math]}$ ；
  
  ②用等式表示线段 $\text{[math]}$ 、 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系，并证明；
2. （2）当 $\text{[math]}$ 时，直接用等式表示线段 $\text{[math]}$ 、 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系是．
答案解析收藏纠错 + 选题
28. (2020·密云模拟) 对于平面直角坐标系 $\text{[math]}$ 中的任意一点 $\text{[math]}$ ，给出如下定义：经过点 $\text{[math]}$ 且平行于两坐标轴夹角平分线的直线，叫做点 $\text{[math]}$ 的“特征线”．例如：点 $\text{[math]}$ 的特征线是 $\text{[math]}$ 和 $\text{[math]}$ ．
1. （1）若点 $\text{[math]}$ 的其中一条特征线是 $\text{[math]}$ ，则在 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三个点中，可能是点 $\text{[math]}$ 的点有；
2. （2）已知点 $\text{[math]}$ 的平行于第二、四象限夹角平分线的特征线与 $\text{[math]}$ 轴相交于点 $\text{[math]}$ ，直线 $\text{[math]}$ 经过点 $\text{[math]}$ ，且与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．使 $\text{[math]}$ 的面积不小于6，求 $\text{[math]}$ 的取值范围；
3. （3）已知点 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ 的半径为1．当 $\text{[math]}$ 与点 $\text{[math]}$ 的特征线存在交点时，直接写出 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题