 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 
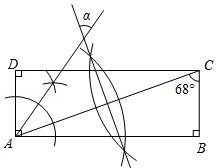
⑴作⊙O的直径AD;(2)以点D为圆心,DO长为半径画弧,交⊙O于B , C两点;(3)连接DB , DC , AB , AC , BC . 根据以上作图过程及所作图形,下列四个结论中错误的是( )

 B .
B . 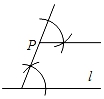 C .
C .  D .
D . 
|
已知:线段a、b, 求作: 作法:如图. |
请您写出上述尺规作图的依据:.
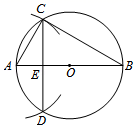
⑴作⊙O的直径AB;
⑵以点A为圆心,AO长为半径画弧,交⊙O于C,D两点;
⑶连接CD交AB于点E,连接AC,BC.
根据以上作图过程及所作图形,有下面三个推断:
①CE=DE; ②BE=3AE; ③BC=2CE.
所有正确推断的序号是.
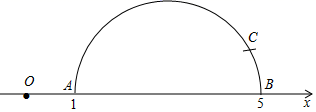
第一步:在数轴上,点O表示数0,点A表示数1,点B表示数5,以AB为直径作半圆(如图);
第二步:以B点为圆心,1为半径作弧交半圆于点C(如图);
第三步:以A点为圆心,AC为半径作弧交数轴的正半轴于点M.
请你在下面的数轴中完成第三步的画图(保留作图痕迹,不写画法),并写出点M表示的数为.

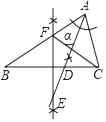
①将半径2的⊙O六等分,依次得到A,B,C,D,E,F六个分点;
②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;
③连结OG.
问:OG的长是多少?大臣给出的正确答案是
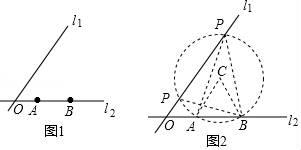
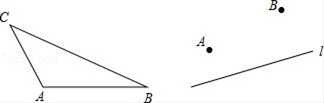
如图1,直线L1与L2相交于点O,A,B是L2上两点,点P是直线L1上的点,且∠APB=30°,请在图中作出符合条件的点P.
作法:如图2,
⑴以AB为边在L2上方作等边△ABC;
⑵以C为圆心,AB长为半径作⊙C交直线L1于P1 , P2两点.则P1、P2就是所作出的符合条件的点P.
请回答:该作图的依据是.



求作: ,使
,
,(用尺规作图,保留作图痕迹,不写作法).
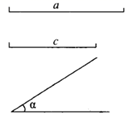
请你根据所学的知识,说明尺规作图作出 ,用到的是三角形全等判定定理中的_▲_,作出的
是唯一的,依据是三角形全等判定定理中的_▲_.
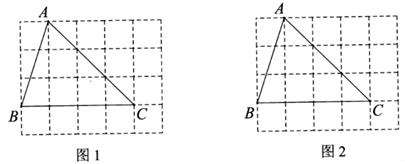

(1)在图1中画 ,使格点G,H分别在边
,
上,且均不与点A,B,C,D重合.
(2)在图2中,在线段 上找一格点
,使得
.
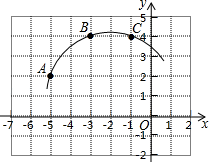
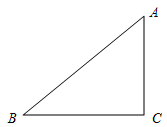

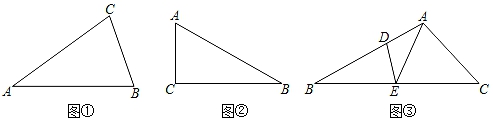
①求∠B和∠C的关系式.
②求∠BAC的取值范围.