初中数学苏科版八年级下册第九章中心对称图形单元测试卷

更新时间：2021-05-24 浏览次数：130 类型：单元试卷

一、单选题

1. (2021八下·北仑期中) 下列图形中，既是轴对称图形又是中心对称图形的有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
2. (2020八下·涪陵期末) 下列命题是假命题的是（）

A . 对角线互相平分的四边形是平行四边形 B . 对角线相等的平行四边形是矩形 C . 对角线互相垂直的四边形是菱形 D . 对角线互相垂直平分且相等的四边形是正方形

答案解析收藏纠错 + 选题
3. (2021八下·姜堰期中) 如图，在△ABC中，∠BAC＝105º，将△ABC绕点A按逆时针方向旋转得到△ADE，若点D恰好落在边BC上，且AD＝CD，则∠C的度数为（）

A . 25º B . 30º C . 35º D . 40º

答案解析收藏纠错 + 选题
4. (2021八下·慈溪期中) 如图，平行四边形ABCD的对角线AC与BD相交于点O ， AE⊥BC ，垂足为E ， $\text{[math]}$ ，AC＝2，BD＝4，则AE的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021八下·北仑期中) 如图，在平行四边形 $\text{[math]}$ 中，点A₁ ， A₂ ， A₃ ， A₄和C₁ ， C₂ ， C₃ ， C₄分别是AB和CD的五等分点，点B₁ ， B₂和D₁ ， D₂分别是BC和DA的三等分点，已知四边形A₄B₂C₄D₂的面积为2，则平行四边形ABCD的面积为（）

A . 4 B . $\text{[math]}$ C . $\text{[math]}$ D . 30

答案解析收藏纠错 + 选题
6. (2021八下·重庆开学考) 如图，菱形ABCD的边长是4cm，且∠ABC＝60°，E是BC中点，P点在BD上，则PE+PC的最小值为（）cm.

A . 2 B . 2 $\text{[math]}$ C . 3 D . 4

答案解析收藏纠错 + 选题
7. (2023八上·萧山月考) 如图，在△ABC中，∠ACB＝90°，以△ABC的各边为边作三个正方形，点G落在HI上，若AC＋BC＝6，空白部分面积为10.5，则AB的长为（）

A . 3 $\text{[math]}$ B . $\text{[math]}$ C . 2 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021八下·慈溪期中) 如图，已知▱OABC的顶点A，C分别在直线 $\text{[math]}$ 和 $\text{[math]}$ 上，O是坐标原点，则对角线OB长的最小值为（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
9. (2021八下·营口期末) 矩形ABCD与ECFG如图放置，点B ， C ， F共线，点C ， E ， D共线，连接AG ，取AG的中点H，连接EH ．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024八上·龙江期末) 如图，正方形 $\text{[math]}$ 的面积为 $\text{[math]}$ ， $\text{[math]}$ 是等边三角形，点 $\text{[math]}$ 在正方形 $\text{[math]}$ 内，在对角线 $\text{[math]}$ 上有一点 $\text{[math]}$ ，使 $\text{[math]}$ 的和最小，则这个最小值为（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2020八上·东台月考) 如图， $\text{[math]}$ 按顺时针方向转动40°得 $\text{[math]}$ ，点D恰好在边BC上，则∠C＝°.

答案解析收藏纠错 + 选题
12. (2020八下·海州期末) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ 、 $\text{[math]}$ 相交于点 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点.若 $\text{[math]}$ ，则 $\text{[math]}$ 的长是 $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2020八下·福州期中) 在平面直角坐标系 $\text{[math]}$ 中，已知点 $\text{[math]}$ ， $\text{[math]}$ ，请确定点C的坐标，使得以A ， B ， C ， O为顶点的四边形是平行四边形，则满足条件的所有点C的坐标是．

答案解析收藏纠错 + 选题
14. (2021八下·姜堰期中) 如图，在菱形ABCD中，对角线AC、BD交于点O，过点A作AM⊥CD于点M，已知AC＝6，BD＝8，则AM＝.

答案解析收藏纠错 + 选题
15. (2021八下·上海期中) 如图，□ $\text{[math]}$ 的周长为 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，则 $\text{[math]}$ 的周长为 $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2020八上·咸阳开学考) 如图，在长方形ABCD中，AB＝12，BC＝9，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE＝OD，则AP＝.

答案解析收藏纠错 + 选题
17. (2021八下·北仑期中) 如图，△ABC中，AB＝4，AC＝3，AD、AE分别是其角平分线和中线，过点C作CG⊥AD于F，交AB于G，连接EF，则线段EF的长为

答案解析收藏纠错 + 选题
18. (2020八下·天桥期末) 如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M不与点B，C重合），过点C作CN⊥DM交AB于点N，连结OM、ON，MN．下列五个结论：①△CNB≌△DMC；②ON＝OM；③ON⊥OM；④若AB＝2，则S_△_OMN的最小值是1；⑤AN²+CM²＝MN² ．其中正确结论是；（只填序号）

答案解析收藏纠错 + 选题

三、综合题

19. (2021八下·贺兰期中) 在下列网格图中，每个小正方形的边长均为1个单位．在Rt△ABC中，∠C＝90°，AC＝3，BC＝4．

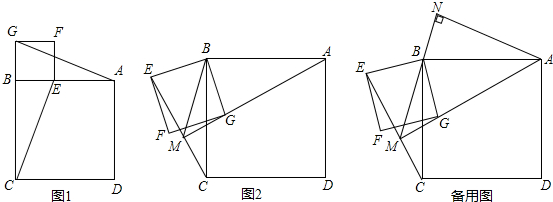
（1）试在图中做出△ABC以A为旋转中心，沿顺时针方向旋转90°后的图形△A₁B₁C₁；
（2）若点B的坐标为（﹣3，5），试在图中画出直角坐标系，并写出 A、C两点的坐标；
（3）根据（2）的坐标系作出与△ABC关于原点对称的图形△A₂B₂C₂ ，并写出B₂、C₂两点的坐标．

答案解析收藏纠错 + 选题
20. (2024八下·谷城月考) 如图，四边形ABCD是平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E.
1. （1）求证：BE＝CD；
2. （2）若BF恰好平分∠ABE，连接AC、DE，求证：四边形ACED是平行四边形.
答案解析收藏纠错 + 选题
21. (2020八下·三台期末) 如图，在Rt $\text{[math]}$ ABC中，∠ACB＝90°．过点C的直线m∥AB，D为AB边上一点，过点D作DE⊥BC交直线m于点E，垂足为点F，连结CD、BE．
1. （1）求证：CE＝AD
2. （2）当点D是AB中点时，四边形BECD是什么特殊四边形？说明你的理由；
3. （3）若点D是AB中点，当四边形BECD是正方形时，则∠A大小满足什么条件？
答案解析收藏纠错 + 选题
22. (2020八下·花都期末) 如图①，在矩形OACB中，点A、B分别在x轴、y轴正半轴上，点C在第一象限，OA＝8，OB＝6．
1. （1）请直接写出点C的坐标；
2. （2）如图②，点F在BC上，连接AF，把 $\text{[math]}$ ACF沿着AF折叠，点C刚好与线段AB上一点 $\text{[math]}$ 重合，求线段CF的长度；
3. （3）如图③，动点P(x，y)在第一象限，且y＝2x﹣6，点D在线段AC上，是否存在直角顶点为P的等腰直角 $\text{[math]}$ BDP，若存在，请求出点P的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
23. (2020八下·大石桥期末) △ABC中，点O是AC上一动点，过点O作直线MN $\text{[math]}$ BC，若MN交∠BCA的平分线于点E，交∠DCA的平分线于点F，连接AE、AF.
1. （1）说明： $\text{[math]}$ ；
2. （2）当点O运动到AC中点处时，求证：四边形AECF是矩形；
3. （3）在（2）的条件下，当△ABC满足什么条件时，四边形AECF为正方形，并加以证明.
答案解析收藏纠错 + 选题
24. (2020八下·灵丘期末) 已知：如图已知直线 $\text{[math]}$ 的函数解析式为 $\text{[math]}$ ，与x轴交于点A，与y轴交于点B．
1. （1）求A、B两点的坐标；
2. （2）若点 $\text{[math]}$ 为线段 $\text{[math]}$ 上的一个动点（与A、B不重合），作 $\text{[math]}$ 轴于点E， $\text{[math]}$ 轴于点F，连接 $\text{[math]}$ ，问：
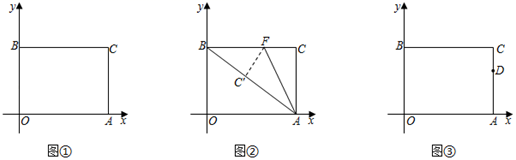
  ①若 $\text{[math]}$ 的面积为S，求S关于m的函数关系式，并写出m的取值范围；
  
  ②是否存在点P，使 $\text{[math]}$ 的值最小？若存在，求出 $\text{[math]}$ 的最小值；若不存在，请说明理由．
答案解析收藏纠错 + 选题
25. (2020八下·金牛期末) 已知四边形ABCD为矩形，对角线AC、BD相交于点O，∠CDO＝30°．点E、F为矩形边上的两个动点，且∠EOF＝60°．
1. （1）如图1，当点E、F分别位于AB、AD边上时．
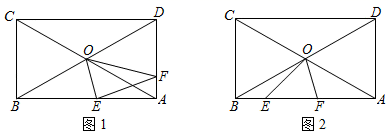
  ①求证：∠DOF＝∠AOE；
  
  ②若∠OEB＝75°，求证：DF＝AE．
2. （2）如图2，当点E、F同时位于AB边上时，若∠OFB＝75°，试探究线段AF与线段BE的数量关系，并说明理由．
答案解析收藏纠错 + 选题
26. (2020八下·济南期末) 如图，四边形ABCD、BEFG均为正方形，
1. （1）如图1，连接AG、CE，试判断AG和CE的数量和位置关系并证明.
2. （2）将正方形BEFG绕点B顺时针旋转β角（0°＜β＜180°），如图2，连接AG、CE相交于点M，连接MB，当角β发生变化时，∠EMB的度数是否发生变化？若不变化，求出∠EMB的度数；若发生变化，请说明理由.
3. （3）在（2）的条件下，过点A作AN⊥MB交MB的延长线于点N，请直接写出线段CM与BN的数量关系.
答案解析收藏纠错 + 选题