
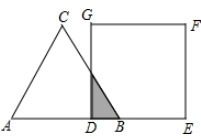
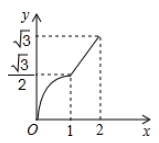
 B .
B . 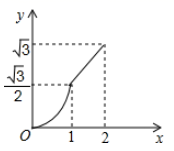 C .
C . 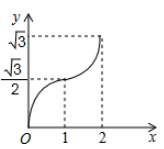 D .
D . 

|
进价(元/个) |
售价(元/个) |
销量(个/日) |
|
|
A型 |
400 |
600 |
200 |
|
B型 |
800 |
1200 |
400 |
根据市场行情,该销售商对A型手写板降价销售,同时对B型手写板提高售价,此时发现A型手写板每降低5元就可多卖1个,B型手写板每提高5元就少卖1个.销售时保持每天销售总量不变,设其中A型手写板每天多销售x个,每天获得的总利润为y元.
