



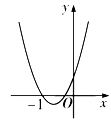
 B .
B . 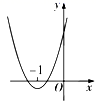 C .
C . 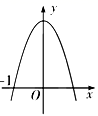 D .
D . 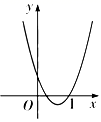
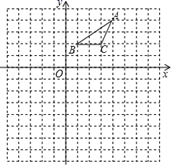
⑴画出△ABC关于y轴对称的△A1B1C1 , 并写出点B1的坐标;
⑵在给定的网格中,以点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2 , 画出△A2B2C2;并写出点B2的坐标.

|
等级 |
成绩n/分 |
频数 |
|
A |
94.5<n≤100 |
2 |
|
89.5<n<94.5 |
||
|
B |
84.5<n<89.5 |
6 |
|
79.5<n<84.5 |
14 |
|
|
C |
74.5<n<79.5 |
16 |
|
69.5<n<74.5 |
||
|
D |
64.5<n<69.5 |
3 |
|
59.5<n<64.5 |
2 |


①求证:DQ=AE;
②推断: 的值为;