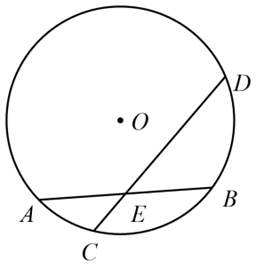
 B .
B .  C .
C .  D .
D . 

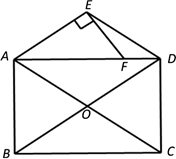
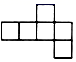 B .
B . 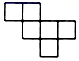 C .
C . 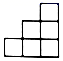 D .
D . 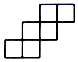


①数据收集,抽取的20名学生阅读关于两会文章的篇数如下(单位:篇):5,3,3,4,5,4,6,7,4,6,6,7,6,5,4,5,5,6,4,6.
②数据整理,将收集的数据进行分组并绘制成不完整的扇形统计图:
|
阅读的篇数(篇) |
3 |
4 |
5 |
6 |
7 |
|
人数 |
2 |
a |
5 |
6 |
2 |
③数据分析(单位:篇):
|
众数 |
中位数 |
平均数 |
|
6 |
m |
n |
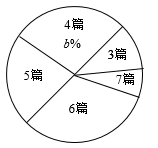
依据统计信息回答问题:


②若△AOB和△COD中有一个是直角三角形时,求△COD与△AOB面积之差;