吉林省2021年中考数学试卷

更新时间：2024-07-13 浏览次数：309 类型：中考真卷

一、单选题

1. (2021七上·永吉期中) 化简 $\text{[math]}$ 的结果为（）

A . －1 B . 0 C . 1 D . 2

答案解析收藏纠错 + 选题
2. (2021·吉林) 据《吉林日报》2021年5月14日报道，第一季度一汽集团销售整车70060辆，数据70060用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022·金东模拟) 不等式 $\text{[math]}$ 的解集是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·博乐模拟) 如图，粮仓可以近似地看作由圆锥和圆柱组成，其主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2021·吉林) 如图，四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ，点 $\text{[math]}$ 为边 $\text{[math]}$ 上任意一点（点 $\text{[math]}$ 不与点 $\text{[math]}$ ， $\text{[math]}$ 重合）连接 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数可能为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024七下·莘县期末) 古埃及人的“纸草书”中记载了一个数学问题：一个数，它的三分之二，它的一半，它的七分之一，它的全部，加起来总共是33，若设这个数是 $\text{[math]}$ ，则所列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

7. (2023七下·贵池期末) 计算： $\text{[math]}$ -1＝．

答案解析收藏纠错 + 选题
8. (2024九上·青秀开学考) 因式分解： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
9. (2021·吉林) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
10. (2024九上·西城期中) 若关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有两个相等的实数根，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
11. (2021·吉林) 如图，已知线段 $\text{[math]}$ ，其垂直平分线 $\text{[math]}$ 的作法如下：①分别以点 $\text{[math]}$ 和点 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为半径画弧，两弧相交于 $\text{[math]}$ ， $\text{[math]}$ 两点；②作直线 $\text{[math]}$ ．上述作法中 $\text{[math]}$ 满足的条作为 $\text{[math]}$ 1.（填“ $\text{[math]}$ ”，“ $\text{[math]}$ ”或“ $\text{[math]}$ ”）

答案解析收藏纠错 + 选题
12. (2021·吉林) 如图，在平面直角坐标系中，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，连接 $\text{[math]}$ ，若将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为．

答案解析收藏纠错 + 选题
13. (2023·乾安模拟) 如图，为了测量山坡的护坡石坝高，把一根长为 $\text{[math]}$ 的竹竿 $\text{[math]}$ 斜靠在石坝旁，量出竿上 $\text{[math]}$ 长为 $\text{[math]}$ 时，它离地面的高度 $\text{[math]}$ 为 $\text{[math]}$ ，则坝高 $\text{[math]}$ 为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2024九下·重庆市开学考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为半径画弧，分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，则图中阴影部分的面积为（结果保留 $\text{[math]}$ ）．

答案解析收藏纠错 + 选题

三、解答题

15. (2021·吉林) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2024九上·大安期末) 第一盒中有1个白球、1个黑球，第二盒中有1个白球，2个黑球．这些球除颜色外无其他差别，分别从每个盒中随机取出1个球，用画树状图或列表的方法，求取出的2个球都是白球的概率．

答案解析收藏纠错 + 选题
17. (2021·吉林) 如图，点D在AB上，点E在AC上，BE和CD相交于点O ， AB＝AC ， ∠B＝∠C.求证：AD＝AE

答案解析收藏纠错 + 选题
18. (2022七下·大庆期末) 港珠澳大桥是世界上最长的跨海大桥，它由桥梁和隧道两部分组成，桥梁和隧道全长共 $\text{[math]}$ ．其中桥梁长度比隧道长度的9倍少 $\text{[math]}$ ．求港珠澳大桥的桥梁长度和隧道长度．

答案解析收藏纠错 + 选题
19. (2021·吉林) 图①、图2均是 $\text{[math]}$ 的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，点 $\text{[math]}$ ，点 $\text{[math]}$ 均在格点上，在给定的网格中按要求画图，所画图形的顶点均在格点上．
1. （1）在图①中，以点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点画一个等腰三角形；
2. （2）在图②中，以点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点画一个面积为3的平行四边形．
答案解析收藏纠错 + 选题
20. (2021·吉林) 2020年我国是全球主要经济体中唯一实现经济正增长的国家，各行各业蓬勃发展，其中快递业务保持着较快的增长．给出了快递业务的有关数据信息．

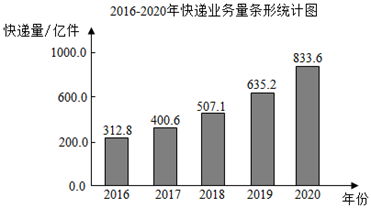
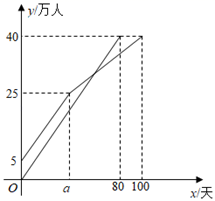
2016﹣2017年快递业务量增长速度统计表

年龄

2016

2017

2018

2019

2020

增长速度

51.4%

28.0%

26.6%

25.3%

31.2%

说明：增长速度计算办法为：增长速度=（本年业务量-去年业务量）÷去年业务量×100%．

根据图中信息，解答下列问题：
1. （1） 2016﹣2020年快递业务量最多年份的业务量是亿件．
2. （2） 2016﹣2020年快递业务量增长速度的中位数是．
3. （3）下列推断合理的是（填序号）．
  ①因为2016﹣2019年快递业务量的增长速度逐年下降，所以预估2021年的快递业务量应低于2020年的快递业务量；
  
  ②因为2016﹣2020年快递业务量每年的增长速度均在25%以上．所以预估2021年快递业务量应在 $\text{[math]}$ 亿件以上．
答案解析收藏纠错 + 选题
21. (2022·南城模拟) 如图，在平面直角坐标系中，一次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴相交于点 $\text{[math]}$ ，与反比例函数 $\text{[math]}$ 在第一象限内的图象相交于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴于点 $\text{[math]}$ ．
1. （1）求反比例函数的解析式；
2. （2）求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
22. (2021·吉林) 数学小组研究如下问题：长春市的纬度约为北纬 $\text{[math]}$ ，求北纬 $\text{[math]}$ 纬线的长度，小组成员查阅了相关资料，得到三条信息：
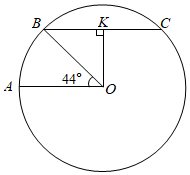
⑴在地球仪上，与南，北极距离相等的大圆圈，叫赤道，所有与赤道平行的圆圈叫纬线；

⑵如图， $\text{[math]}$ 是经过南、北极的圆，地球半径 $\text{[math]}$ 约为 $\text{[math]}$ ．弦 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．若 $\text{[math]}$ ，则以 $\text{[math]}$ 为半径的圆的周长是北纬 $\text{[math]}$ 纬线的长度；

⑶参考数据： $\text{[math]}$ 取3， $\text{[math]}$ ， $\text{[math]}$ ．

小组成员给出了如下解答，请你补充完整：

解：因为 $\text{[math]}$ ， $\text{[math]}$ ，

所以 $\text{[math]}$ （        ）（填推理依据），

因为 $\text{[math]}$ ，所以 $\text{[math]}$ ，

在 $\text{[math]}$ 中， $\text{[math]}$ ．

$\text{[math]}$       ▲      （填“ $\text{[math]}$ ”或“ $\text{[math]}$ ”）．

所以北纬 $\text{[math]}$ 的纬线长 $\text{[math]}$

$\text{[math]}$ ▲   （填相应的三角形函数值）

$\text{[math]}$    ▲   （ $\text{[math]}$ ）（结果取整数）．

答案解析收藏纠错 + 选题
23. (2022八下·霍州期末) 疫苗接种，利国利民．甲、乙两地分别对本地各40万人接种新冠疫苗．甲地在前期完成5万人接种后，甲、乙两地同时以相同速度接种，甲地经过 $\text{[math]}$ 天后接种人数达到25万人，由于情况变化，接种速度放缓，结果100天完成接种任务，乙地80天完成接种任务，在某段时间内，甲、乙两地的接种人数 $\text{[math]}$ （万人）与各自接种时间 $\text{[math]}$ （天）之间的关系如图所示．
1. （1）直接写出乙地每天接种的人数及 $\text{[math]}$ 的值；
2. （2）当甲地接种速度放缓后，求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式，并写出自变量 $\text{[math]}$ 的取值范围；
3. （3）当乙地完成接种任务时，求甲地未接种疫苗的人数．
答案解析收藏纠错 + 选题
24. (2021·吉林) 如图①，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是斜边 $\text{[math]}$ 上的中线，点 $\text{[math]}$ 为射线 $\text{[math]}$ 上一点，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，点 $\text{[math]}$ 的对应点为点 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ．直接写出 $\text{[math]}$ 的长（用含 $\text{[math]}$ 的代数式表示）；
2. （2）若 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，点 $\text{[math]}$ 与点 $\text{[math]}$ 在直线 $\text{[math]}$ 的异侧，连接 $\text{[math]}$ ，如图②，判断四边形 $\text{[math]}$ 的形状，并说明理由；
3. （3）若 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
25. (2021·吉林) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发沿折线 $\text{[math]}$ 向终点 $\text{[math]}$ 运动，在边 $\text{[math]}$ 上以 $\text{[math]}$ 的速度运动；在边 $\text{[math]}$ 上以 $\text{[math]}$ 的速度运动，过点 $\text{[math]}$ 作线段 $\text{[math]}$ 与射线 $\text{[math]}$ 相交于点 $\text{[math]}$ ，且 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．设点 $\text{[math]}$ 的运动时间为 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 重合部分图形的面积为 $\text{[math]}$ ．
1. （1）当点 $\text{[math]}$ 与点 $\text{[math]}$ 重合时，直接写出 $\text{[math]}$ 的长；
2. （2）当点 $\text{[math]}$ 在边 $\text{[math]}$ 上运动时，直接写出 $\text{[math]}$ 的长（用含 $\text{[math]}$ 的代数式表示）；
3. （3）求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式，并写出自变量 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
26. (2021·吉林) 如图，在平面直角坐标系中，二次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ，点 $\text{[math]}$ ．
1. （1）求此二次函数的解析式；
2. （2）当 $\text{[math]}$ 时，求二次函数 $\text{[math]}$ 的最大值和最小值；
3. （3）点 $\text{[math]}$ 为此函数图象上任意一点，其横坐标为 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴，点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ．已知点 $\text{[math]}$ 与点 $\text{[math]}$ 不重合，且线段 $\text{[math]}$ 的长度随 $\text{[math]}$ 的增大而减小．
  ①求 $\text{[math]}$ 的取值范围；
  
  ②当 $\text{[math]}$ 时，直接写出线段 $\text{[math]}$ 与二次函数 $\text{[math]}$ 的图象交点个数及对应的 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题