 B .
B .  C .
C .  D .
D . 
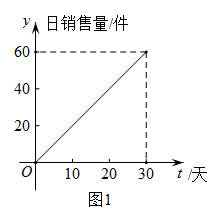


①一次函数 的图象与线段
有公共点;
②当 时,一次函数
的图象与线段
有公共点;
③当 时,一次函数
的图象与线段
有公共点;
④当 时,一次函数
的图象与线段
有公共点.
上述说法中正确的是(填序号).

求作:菱形 使其两条对角线的长分别等于线段
的长.
作法:①如图1,作线段 的垂直平分线
,交线段
于点
;

②如图2,作射线 ,在
上截取线段
;
③作线段 的垂直平分线
交线段
于点
;
④以点 为圆心,线段
的一半为半径作弧,交直线
于点
;
⑤连接 .
四边形
就是所求作的菱形.
问题:

证明: ,
四边形
是_
四边形
是菱形.()(填推理的依据).
a.收集数据
⑴班
⑵班
b.整理和描述数据
| 成绩 | ⑴班 | ⑵班 | ||
| 频数 | 频率 | 频数 | 频率 | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
注:成绩 分及以上为优秀,
分为合格,
分以下为不合格.
c.分析数据
两组样本数据的平均数、中位数、众数如下表所示:
| 班级 | 平均数 | 众数 | 中位数 |
| ⑴班 | | | |
| ⑵班 | | | |
根据以上信息,回答下列问题:
①当 时,求区域“
”内整点的个数;
②如果区域“ ”内恰好有
个整点,直接写出
的取值范围.
①依题意补全图1;

②猜想 与
之间的数量关系,并证明.
