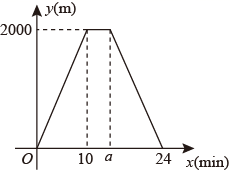
 B .
B .  C .
C .  D .
D . 
![]()



|
次数 成绩 学生 |
第1次 |
第2次 |
第3次 |
第4次 |
第5次 |
第6次 |
第7次 |
第8次 |
|
甲 |
169 |
165 |
168 |
169 |
172 |
173 |
169 |
167 |
|
乙 |
161 |
174 |
172 |
162 |
163 |
172 |
172 |
176 |
两名同学的8次跳高成绩数据分析如下表:
|
名称 成绩 学生 |
平均数 (单位:cm) |
中位数 (单位:cm) |
众数 (单位:cm) |
方差 (单位:cm2) |
|
甲 |
a |
b |
c |
5.75 |
|
乙 |
169 |
172 |
172 |
31.25 |
根据图表信息回答下列问题: