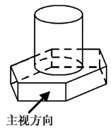
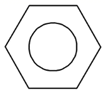
 B .
B .  C .
C . 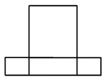 D .
D . 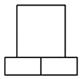
 B .
B . 
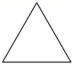 B .
B .  C .
C . 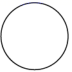 D .
D . 
 B .
B .  C .
C . 
 C .
C .  D .
D . 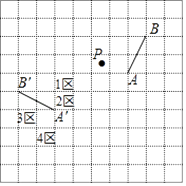
![]()
①判断 和
的数量关系,并证明;
②求证: .
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°≈( )2+(
)2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.