初中数学浙教版九年级上册第3章 圆的基本性质单元检测

如图，在⊙O中，D、E分别是半径OA、OB的中点，C是⊙O上一点，CD=CE．

（1）求证：=；

（2）若∠AOB=120°，CD=2 ， 求半径OA的长．

如图，在⊙O的内接四边形ABCD中，AB=AD，∠C=120°，点E在上．

（1）求∠E的度数；

（2）连接OD、OE，当∠DOE=90°时，AE恰好为⊙O的内接正n边形的一边，求n的值

将正六边形纸片按下列要求分割（每次分割纸片不得剩余）

第一次：将正六边形纸片分割成三个全等的菱形，然后选取其中一个菱形再分割成一个正六边形和两个全等的正三角形．（后面就依次用剩下的正六边形按上述方法分割…）

（1）请画出第一次分割示意图；

（2）若原正六边形的面积为a，请你将第一次，第二次，第三次分割后所得的正六边形的面积填入下表：

（3）猜想：分割后所得的正六边形的面积S与分割次数n有何关系？（S用含a和n的代数式表示）

如图，风车的支杆OE垂直于桌面，风车中心O到桌面的距离OE为25cm，小小风车在风吹动下绕着中心O不停地转动，转动过程中，叶片端点A、B、C、D在同一圆O上，已知⊙O的半径为10cm．

（1）风车在转动过程中，当∠AOE=45°时，求点A到桌面的距离（结果保留根号）．

（2）在风车转动一周的过程中，求点A相对于桌面的高度不超过20cm所经过的路径长（结果保留π）．

我们知道三角形外接圆的圆心叫做三角形的外心，三角形内切圆的圆心叫做三角形的内心．由于三角形的三条高（或高所在的直线）相交于一点，因此我们把三角形三条高的交点叫做三角形的垂心．下面我们以锐角三角形为例，证明三角形的三条高相交于一点．

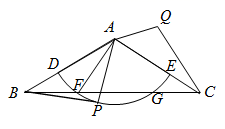
如图，在△ABC中，AD ， BE分别是BC ， AC边上的高，且AD与BE相交于点P ． 连接CP并延长，交AB于点F ．

求证：CF⊥AB ．

证明：分别过点A ， B ， C作它们所对边的平行线，三条平行线两两相交于点M ， N ， Q ． 分别连接PM ， PN ， PQ ．

∵MN BC ， MQ AB ， NQ AC ，

∴四边形MABC ， 四边形ANBC ， 四边形ABQC都是平行四边形．

∴BC=AM=AN ， AC=BN=BQ ， AB=MC=CQ ．

∵AD⊥BC ，

∴∠MAD=∠ADB=90°，即AD⊥MN ．

∴PM=PN ．

…

学习任务：