 B .
B .  D .
D . 

 B .
B .  C .
C .  D .
D . 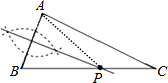
 B .
B .  C .
C . 
 B .
B .  C .
C .  D .
D . 
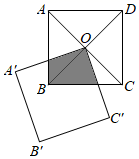
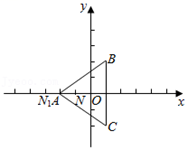

A2 B2 C2


![]()
根据你对例题的理解,解答下列问题:
若数轴上数 表示的点与数1表示的点重合.(根据此情境解决下列问题)




