贵州省六盘水市2021-2022学年九年级上学期第三次月考数...

更新时间：2022-02-16 浏览次数：72 类型：月考试卷

一、单选题

1. (2021九上·六盘水月考) 如图，在 $\text{[math]}$ ABC中，DE $\text{[math]}$ AC，BD＝6cm，DA＝3cm，BE＝4cm，则EC的长为（）

A . 1cm B . 2cm C . 3cm D . 4cm

答案解析收藏纠错 + 选题
2. (2021九上·六盘水月考) 解一元二次方程 $\text{[math]}$ 最适宜的方法是（）

A . 直接开平方 B . 公式法 C . 因式分解法 D . 配方法

答案解析收藏纠错 + 选题
3. (2022·广阳模拟) 如图是一个几何体的实物图，则其主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023九上·诸暨月考) 下列说法正确的是（）

A . 在同一年出生的400名学生中，至少有两人的生日是同一天 B . 某种彩票中奖的概率是1%，买100张这种彩票一定会中奖 C . 天气预报明天下雨的概率是50%，所以明天将有一半的时间在下雨 D . 抛一枚图钉，钉尖着地和钉尖朝上的概率一样大

答案解析收藏纠错 + 选题
5. (2023九上·越秀月考) 已知 $\text{[math]}$ 且对应中线之比为 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 的周长之比为 $\text{[math]}$ 　　 $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021九上·六盘水月考) 一个不透明的盒子里装有120个红、黄两种颜色的小球，这些球除颜色外其他完全相同，每次摸球前先将盒子里的球摇匀任意摸出一个球记下颜色后再放回盒子，通过大量重复摸球试验后发现，摸到黄球的频率稳定在0.3，那么估计盒子中红球的个数为（）

A . 36 B . 48 C . 70 D . 84

答案解析收藏纠错 + 选题
7. (2021九上·平远期末) 同一时刻，小明在阳光下的影长为2米，与他邻近的旗杆的影长为6米，小明的身高为1.6米，则旗杆的高为（　　）

A . 3.2米 B . 4.8米 C . 5.2米 D . 5.6米

答案解析收藏纠错 + 选题
8. (2023九上·丘北月考) 在数学活动课上，老师和同学们判断一个四边形门框是否为矩形.下面是某个合作小组的4位同学拟定的方案，其中正确的是（）

A . 测量对角线是否互相平分 B . 测量两组对边是否分别相等 C . 测量其内角是否均为直角 D . 测量对角线是否垂直

答案解析收藏纠错 + 选题
9. (2021九上·六盘水月考) 如图，在菱形ABCD中，AB＝5，AC＝8，过点B作BE⊥CD于点E，则BE的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 6 D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021八下·濉溪期末) 我们知道方程x²＋2x-3＝0的解是x₁＝1，x₂＝-3，现给出另一个方程(2x＋3)²＋2(2x＋3)-3＝0，它的解是(　　).

A . x₁＝1，x₂＝3 B . x₁＝1，x₂＝-3 C . x₁＝-1，x₂＝3 D . x₁＝-1，x₂＝-3

答案解析收藏纠错 + 选题
11. (2021九上·六盘水月考) 如图所示为某种型号的台灯的横截面图，已知台灯灯柱AB的长为30cm，且与水平桌面垂直，灯臂AC的长为10cm，灯头的横截面 $\text{[math]}$ CEF为直角三角形，当灯臂AC与灯柱AB垂直时，沿CE边射出的光线刚好射到底座B点.若不考虑其他因素，则该台灯在桌面可照亮的宽度BD的长为（）

A . 90cm B . 100cm C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2021九上·六盘水月考) 如图，在正方形ABCD中，E为AB中点，连结DE，过点D作 $\text{[math]}$ 交BC的延长线于点F，连结 $\text{[math]}$ 若 $\text{[math]}$ ，则EF的值为 $\text{[math]}$ $\text{[math]}$

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题

二、填空题

13. (2021九上·六盘水月考) 一元二次方程3x²﹣6x＝2（x﹣2）的根为.

答案解析收藏纠错 + 选题
14. (2021九上·六盘水月考) 为了解某校九年级学生每周的零花钱情况，随机抽取了该校100名九年级学生，他们每周的零花钱x（元）统计如表：
组别（元）
0≤x＜30
30≤x＜50
50≤x＜60
x≥60
人数
16
31
33
20
根据以上结果，随机抽取该校一名学生，估计该学生每周的零花钱在60以上（包含60）的概率为.

答案解析收藏纠错 + 选题
15. (2021九上·六盘水月考) 如图，四边形 $\text{[math]}$ 是正方形，按如下步骤操作：①分别以点A，D为圆心，以 $\text{[math]}$ 长为半径圆弧，两弧交于点P，连接 $\text{[math]}$ ， $\text{[math]}$ ：②连接 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2021九上·六盘水月考) 如图，已知矩形OABC与矩形FEDO是位似图形，P是位似中心，若点A的坐标为（0，6），点E的坐标为（2，3），则点B的坐标为．

答案解析收藏纠错 + 选题

三、解答题

17. (2021九上·六盘水月考) 如图是一个大正方体切去一个小正方体组成的几何体.
1. （1）下列三个图形中，从上面、左面、正面看到的平面图形分别是哪个；（写序号）
2. （2）若大正方体的边长为20cm，小正方体的边长为10cm，求这个几何体的表面积.
答案解析收藏纠错 + 选题
18. (2021九上·六盘水月考) 已知关于x的一元二次方程 $\text{[math]}$ .
1. （1）证明：无论k取何值，该方程总有两个不等的实数根；
2. （2）若该方程的两个实数根分别为x₁ ， x₂ ，且（x₁﹣x₂+2）（x₁﹣x₂﹣2）＝﹣3，求k的值.
答案解析收藏纠错 + 选题
19. (2021九上·六盘水月考) 如图，四边形ABCD∽四边形A₁B₁C₁D₁ ， ∠A＝80°，∠B＝75°，∠C＝125°，求x，∠D₁.

答案解析收藏纠错 + 选题
20. (2021九上·六盘水月考) 网络购物已成为新的消费方式，催生了快递行业的高速发展，某快递公司今年6月份与8月份投递的快递件数分别为10万件和12.1万件，假定每月投递的快递件数的增长率相同．
1. （1）求该快递公司投递的快递件数的月平均增长率．
2. （2）如果每个快递小哥平均每月最多可投递0.8万件快递，该公司现有16个快递小哥，请通过计算说明按此快递件数的增长速度，在不增加人手的情况下，该公司能否完成今年9月份的投递任务．
答案解析收藏纠错 + 选题
21. (2021九上·六盘水月考) 如图，AE∥BF，AC平分∠BAE，且交BF于点C，BD平分∠ABF，且交AE于点D，连接CD．
1. （1）求证：四边形ABCD是菱形；
2. （2）若∠ADB=30°，BD=6，求AD的长．
答案解析收藏纠错 + 选题

22. (2022九上·杭州期中) 有一个圆形转盘，分黑色、白色两个区域.

（1）某人转动转盘，对指针落在黑色区域或白色区域进行了大量试验，得到数据如下表：

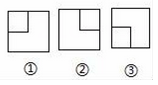
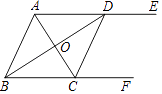
实验次数 $\text{[math]}$ (次)	10	100	2000	5000	10000	50000	100000
白色区域次数 $\text{[math]}$ (次)	3	34	680	1600	3405	16500	33000
落在白色区域频率 $\text{[math]}$	0.3	0.34	0.34	0.32	0.34	0.33	0.33

请你利用上述实验，估计转动该转盘指针落在白色区域的概率为.(精确到0.01)；

（2）若该圆形转盘白色扇形的圆心角为120度，黑色扇形的圆心角为 $\text{[math]}$ ，转动转盘两次，求指针一次落在白色区域，另一次落在黑色区域的概率.

答案解析收藏纠错 + 选题

23. (2021九上·六盘水月考) 如图，矩形ABCD中，AB＝3，BC＝4，E为AD的中点，F为CD上一点，将 $\text{[math]}$ DEF沿EF折叠后，点D恰好落到BF上的点G处，连接BE.
1. （1）求证：BE⊥EF；
2. （2）求折痕EF的长.
答案解析收藏纠错 + 选题
24. (2022九上·金东月考) 如图，在△ABC中，点D，E，F分别在AB，BC，AC边上，DE∥AC，EF∥AB.
1. （1）求证：△BDE∽△EFC.
2. （2）设 $\text{[math]}$ ，
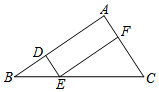
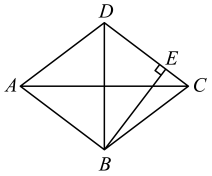
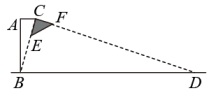
  ①若BC＝12，求线段BE的长；
  
  ②若△EFC的面积是20，求△ABC的面积.
答案解析收藏纠错 + 选题
25. (2021九上·六盘水月考) （一）问题情境：如图1，已知点E，F分别在正方形 $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ ，点M为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）线段 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系是，位置关系是.
2. （2）（二）猜想证明：
  如图2，将线段 $\text{[math]}$ 和 $\text{[math]}$ 绕点B逆时针旋转，旋转角均为 $\text{[math]}$ （ $\text{[math]}$ ）.点M为线段 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，请你判断（1）中的两个结论是否仍然成立.若成立，请证明；若不成立，请说明理由.
3. （3）（三）探索发现：
  将图1中的线段 $\text{[math]}$ 和 $\text{[math]}$ 绕点B逆时针旋转，旋转角为 $\text{[math]}$ ，点M为线段 $\text{[math]}$ 的中点，得到如图3所示的图形，请你判断线段 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系是否发生变化，请说明理由.
答案解析收藏纠错 + 选题