2021-2022学年浙教版数学九下1.2 锐角三角函数的计...

更新时间：2022-02-07 浏览次数：91 类型：同步测试

一、单选题

1. (2021九上·淮北月考) 已知角α为 $\text{[math]}$ ABC的内角，且cosα= $\text{[math]}$ ，则α的取值范围是（）

A . 0°<α<30° B . 30°<α<45° C . 45°<α<60° D . 60°<α<90°

答案解析收藏纠错 + 选题
2. (2021九上·鄞州月考) 如图，已知：45°＜A＜90°，则下列各式成立的是（）

A . sinA=cosA B . sinA＞cosA C . sinA＞tanA D . sinA＜cosA

答案解析收藏纠错 + 选题
3. (2022九上·蓬莱期中) 若用我们数学课本上采用的科学计算器计算sin36 $\text{[math]}$ 18＇，按键顺序正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2021·东营) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若用科学计算器求AC的长，则下列按键顺序正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020九上·舒城期末) 下列各式中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021·静安模拟) 如果锐角 $\text{[math]}$ 的正切值为 $\text{[math]}$ ，那么下列结论中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021九上·渭滨期末) 如图，梯子（长度不变）跟地面所成的锐角为A，关于∠A的三角函数值与梯子的倾斜程度之间，叙述正确的是（）

A . sinA的值越大，梯子越陡 B . cosA的值越大，梯子越陡 C . tanA的值越小，梯子越陡 D . 陡缓程度与∠A的三角函数值无关

答案解析收藏纠错 + 选题
8. 如图，为方便行人推车过天桥，某市政府在 $\text{[math]}$ 高的天桥两端分别修建了 $\text{[math]}$ 长的斜道，用科学计算器计算这条斜道的倾斜角 $\text{[math]}$ ，下列按键顺序正确的是（）．

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2021九上·福山期中) 用计算器求 $\text{[math]}$ 的值，以下按键顺序正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2022·烟台模拟) 已知 $\text{[math]}$ ，运用科学计算器求锐角 $\text{[math]}$ 时（在开机状态下），按下的第一个键是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

11. (2021八下·海珠期中) 如图，在Rt△ABC中，∠C＝90°，BC＝5，AC＝12，则AB＝，∠A＝，∠B＝．（角度精确到1′）

答案解析收藏纠错 + 选题
12. (2021八上·杭州期末) 下列结论中（其中 $\text{[math]}$ ， $\text{[math]}$ 均为锐角），正确的是．（填序号）
① $\text{[math]}$ ；② $\text{[math]}$ ；③当 $\text{[math]}$ 时， $\text{[math]}$ ；④ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2021九上·溧阳期末) 如图，点P在正方形ABCD的BC边上，连接AP，作AP的垂直平分线，交AD延长线于点E，连接PE，交CD于点F.若点F是CD的中点，则tan∠BAP=.

答案解析收藏纠错 + 选题
14. (2021九上·咸阳月考) 若三个锐角 $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ 由小到大的顺序为.

答案解析收藏纠错 + 选题
15. 比较大小： $\text{[math]}$ $\text{[math]}$ （填“ $\text{[math]}$ ”“ $\text{[math]}$ ”）．

答案解析收藏纠错 + 选题
16. (2020·朝阳模拟) 如图所示的网格是正方形网格，则 $\text{[math]}$ $\text{[math]}$ (填“＞”、“=”或“＜”)．

答案解析收藏纠错 + 选题
17. (2020九下·齐齐哈尔期中) 已知 $\text{[math]}$ ，且 $\text{[math]}$ 为锐角，则m的取值范围是．

答案解析收藏纠错 + 选题
18. (2020·高邮模拟) 比较大小： $\text{[math]}$ $\text{[math]}$ (填“ $\text{[math]}$ ”“ $\text{[math]}$ ”或“＞”)

答案解析收藏纠错 + 选题

三、综合题

19. (2020九上·罗庄期末) 如图，AB是⊙O的弦，半径OE⊥AB，P为AB的延长线上一点，PC与⊙O相切于点C，CE与AB交于点F．
1. （1）求证：PC＝PF；
2. （2）连接OB，BC，若OB∥PC，BC＝3 $\text{[math]}$ ，tanP＝ $\text{[math]}$ ，求FB的长．
答案解析收藏纠错 + 选题

20. (2020·烟台) 今年疫情期间，针对各种入口处人工测量体温存在的感染风险高、效率低等问题，清华大学牵头研制一款“测温机器人”，如图1，机器人工作时，行人抬手在测温头处测量手腕温度，体温合格则机器人抬起臂杆行人可通行，不合格时机器人不抬臂杆并报警，从而有效阻隔病原体．

（1）为了设计“测温机器人”的高度，科研团队采集了大量数据．下表是抽样采集某一地区居民的身高数据：

测量对象	男性（18～60岁）			女性（18～55岁）
抽样人数（人）	2000	5000	20000	2000	5000	20000
平均身高（厘米）	173	175	176	164	165	164

根据你所学的知识，若要更准确的表示这一地区男、女的平均身高，男性应采用厘米，女性应采用厘米；

（2）如图2，一般的，人抬手的高度与身高之比为黄金比时给人的感觉最舒适，由此利用（1）中的数据得出测温头点P距地面105厘米．指示牌挂在两臂杆AB，AC的连接点A处，A点距地面110厘米．臂杆落下时两端点B，C在同一水平线上，BC＝100厘米，点C在点P的正下方5厘米处．若两臂杆长度相等，求两臂杆的夹角．

（参考数据表）

计算器按键顺序	计算结果（近似值）	计算器按键顺序	计算结果（近似值）
	0.1		78.7
	0.2		84.3
	1.7		5.7
	3.5		11.3

答案解析收藏纠错 + 选题

21. (2020九下·镇江月考)
1. （1）完成下列表格，并回答下列问题，
  
  锐角 $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
2. （2）当锐角 $\text{[math]}$ 逐渐增大时， $\text{[math]}$ 的值逐渐， $\text{[math]}$ 的值逐渐， $\text{[math]}$ 的值逐渐．
3. （3） $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ；
4. （4） $\text{[math]}$ ；
5. （5） $\text{[math]}$ ；
6. （6）若 $\text{[math]}$ ，则锐角 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
22. (2019·江西) 图1是一台实物投影仪，图2是它的示意图，折线 $\text{[math]}$ 表示固定支架， $\text{[math]}$ 垂直水平桌面 $\text{[math]}$ 于点 $\text{[math]}$ ，点 $\text{[math]}$ 为旋转点， $\text{[math]}$ 可转动，当 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转时，投影探头 $\text{[math]}$ 始终垂直于水平桌面 $\text{[math]}$ ，经测量： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．（结果精确到0.1）
1. （1）如图2， $\text{[math]}$ ， $\text{[math]}$ ．
  ①填空： $\text{[math]}$ °；
  
  ②求投影探头的端点 $\text{[math]}$ 到桌面 $\text{[math]}$ 的距离．
2. （2）如图3，将（1）中的 $\text{[math]}$ 向下旋转，当投影探头的端点 $\text{[math]}$ 到桌面 $\text{[math]}$ 的距离为 $\text{[math]}$ 时，求 $\text{[math]}$ 的大小．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
答案解析收藏纠错 + 选题
23. (2019九上·灵石期末) 某“综合与实践”小组开展了测量本校旗杆高度的实践活动，他们制订了测量方案，并利用课余时间完成了实地测量.他们在旗杆底部所在的平地上，选取两个不同测点，分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差，小组在测量仰角的度数以及两个测点之间的距离时，都分别测量了两次并取它们的平均值作为测量结果，测量数据如下表(不完整)
1. （1）任务一：两次测量A，B之间的距离的平均值是m.
2. （2）任务二：根据以上测量结果，请你帮助“综合与实践”小组求出学校学校旗杆GH的高度.
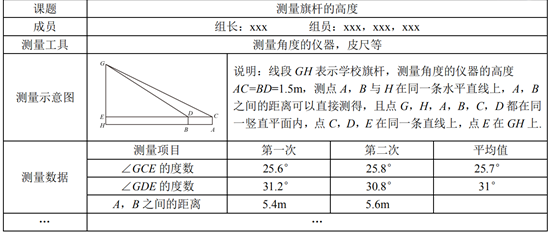
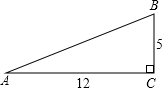
  (参考数据：sin25.7°≈0.43，cos25.7°≈0.90，tan25.7°≈0.48，sin31°≈0.52，cos31°≈0.86，tan31°≈0.60)
3. （3）任务三：该“综合与实践”小组在定制方案时，讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案，但未被采纳.你认为其原因可能是什么？(写出一条即可).
答案解析收藏纠错 + 选题
24. (2019·烟台) 如图所示，一种适用于笔记本电脑的铝合金支架，边 $\text{[math]}$ ， $\text{[math]}$ 可绕点 $\text{[math]}$ 开合，在 $\text{[math]}$ 边上有一固定点 $\text{[math]}$ ，支柱 $\text{[math]}$ 可绕点 $\text{[math]}$ 转动，边 $\text{[math]}$ 上有六个卡孔，其中离点 $\text{[math]}$ 最近的卡孔为 $\text{[math]}$ ，离点 $\text{[math]}$ 最远的卡孔为 $\text{[math]}$ .当支柱端点 $\text{[math]}$ 放入不同卡孔内，支架的倾斜角发生变化.将电脑放在支架上，电脑台面的角度可达到六档调节，这样更有利于工作和身体健康.现测得 $\text{[math]}$ 的长为 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ ，支柱 $\text{[math]}$ 为 $\text{[math]}$ .
1. （1）当支柱的端点 $\text{[math]}$ 放在卡孔 $\text{[math]}$ 处时，求 $\text{[math]}$ 的度数；
2. （2）当支柱的端点 $\text{[math]}$ 放在卡孔 $\text{[math]}$ 处时， $\text{[math]}$ ，若相邻两个卡孔的距离相同，求此间距.(结果精确到十分位)
答案解析收藏纠错 + 选题
25. (2019·达州) 如图1，已知抛物线 $\text{[math]}$ 过点 $\text{[math]}$ ．
1. （1）求抛物线的解析式及其顶点C的坐标；
2. （2）设点D是x轴上一点，当 $\text{[math]}$ 时，求点D的坐标；
3. （3）如图2．抛物线与y轴交于点E，点P是该抛物线上位于第二象限的点，线段PA交BE于点M，交y轴于点N， $\text{[math]}$ 和 $\text{[math]}$ 的面积分别为 $\text{[math]}$ ，求 $\text{[math]}$ 的最大值．
答案解析收藏纠错 + 选题
26. (2020·舟山模拟) 已知在梯形ABCD中，AD∥BC ， AC＝BC＝10，cos∠ACB＝ $\text{[math]}$ ，点E在对角线AC上（不与点A、C重合），∠EDC＝∠ACB ， DE的延长线与射线CB交于点F ，设AD的长为x ．
1. （1）如图1，当DF⊥BC时，求AD的长；
2. （2）设EC＝y ，求y关于x的函数解析式，并直接写出定义域；
3. （3）当△DFC是等腰三角形时，求AD的长．
答案解析收藏纠错 + 选题