重庆市北碚区西南大学附中2021年中考数学四模试卷

更新时间：2022-05-05 浏览次数：111 类型：中考模拟

一、单选题

1. (2024九上·吴桥期末) sin60°=（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021·北碚模拟) 某一次函数的图象与y轴交于正半轴，这个一次函数的表达式可能是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021·北碚模拟) 如图，AB是⊙O的直径，点D在⊙O上，若∠AOC＝120°，则∠BDC的度数是（　　）

A . 20° B . 30° C . 40° D . 45°

答案解析收藏纠错 + 选题
4. (2021·北碚模拟) 函数y＝ $\text{[math]}$ 中自变量x的取值范围是（）

A . x≥3 B . x≤3 C . x≠3 D . x＞3

答案解析收藏纠错 + 选题
5. (2021·北碚模拟) 若x＝2021是关于x的一元二次方程ax²﹣2bx﹣1＝0的一个根，则2020﹣4042b+2021²a的值为（　　）

A . 2019 B . 2020 C . 2021 D . 2022

答案解析收藏纠错 + 选题
6. (2021·北碚模拟) 下列各项变形是因式分解的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021·北碚模拟) 如图，在直角坐标系中， $\text{[math]}$ 的顶点为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．以点O为位似中心，在第三象限内作与 $\text{[math]}$ 的位似比为 $\text{[math]}$ 的位似图形 $\text{[math]}$ ，则点C的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021·北碚模拟) 下列各命题是真命题的是（）

A . 矩形的对称轴是两条对角线所在的直线 B . 平行四边形一定是中心对称图形 C . 有一个内角为60°的平行四边形是菱形 D . 三角形的外角等于它的两个内角之和

答案解析收藏纠错 + 选题
9. (2021·北碚模拟) 我校兴趣小组同学为测量校外“御墅临枫”的一栋电梯高层AB的楼高，从校前广场的C处测得该座建筑物顶点A的仰角为45°，沿着C向上走到30 $\text{[math]}$ 米处的D点．再测得顶点A的仰角为22°，已知CD的坡度：i=1：2，A、B、C、D在同一平面内，则高楼AB的高度为（　　）（参考数据；sin22°≈0.37，cos22°≈0.93，tan22°≈0.40）

A . 60 B . 70 C . 80 D . 90

答案解析收藏纠错 + 选题
10. (2021·北碚模拟) 一辆轿车和一辆货车分别从甲、乙两地同时出发，匀速相向而行，相遇后继续前行，已知两车相遇时轿车比货车多行驶了90千米，设行驶的时间为x（小时），两车之间的距离为y（千米），图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系．则点C的纵坐标是（　　）

A . 260 B . 280 C . 300 D . 320

答案解析收藏纠错 + 选题
11. (2021·北碚模拟) 如果关于x的不等式组 $\text{[math]}$ 有且只有四个整数解，且关于x的分式方程 $\text{[math]}$ 的解为非负数，则符合条件的所有整数a的个数（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
12. (2021·北碚模拟) 如图，菱形OABC的顶点C的坐标为（3，0），D为AO上一点，连接BD，CD，OB，CD与OB相交于点E，取EC的三等分点F（EF＞FC），连接OF并延长，交BC于点G，已知S_△BOD：S_△BOC＝2：3，反比例函数y＝ $\text{[math]}$ （k＞0）经过D，G两点，则k的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2021·北碚模拟) 2020年6月23日，我国的北斗卫星导航系统（BDS）星座部署完成，其中一颗中高轨道卫星高度大约是21500000米．将数字21500000用科学记数法表示为．

答案解析收藏纠错 + 选题
14. (2022九下·阳新模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2021·北碚模拟) 两个人做游戏，每个人都从 $\text{[math]}$ ， 1， $\text{[math]}$ 这三个数中随机选择一个写在纸上，则两人所写的三个数绝对值相等的概率为．

答案解析收藏纠错 + 选题
16. (2022·青岛模拟) 如图，已知在矩形ABCD中，AB＝2，以点A为圆心，AD长为半径作 $\text{[math]}$ ，交AB于点E，以AB为直径的半圆恰好与DC相切，则图中阴影部分的面积为．

答案解析收藏纠错 + 选题
17. (2021·北碚模拟) △ABC中，∠BAC=45°，D为AB上一点，BD=10 $\text{[math]}$ ，连接CD，将△CBD沿CD翻折至△CDF，点B的对应点F点恰好落在边AC上．延长CA至点E，连接DE，若AE=2，tan∠BCD= $\text{[math]}$ ，则DE长为．

答案解析收藏纠错 + 选题
18. (2021·北碚模拟) 为让市民感受春天，中央公园管委会决定圈出一块地打造一片花园，花园中种植桃花，樱花，李花供市民欣赏．经过一段时间，花园中已种植的桃花，樱花，李花面积之比为 $\text{[math]}$ ．根据市民的喜爱程度，将在花园的余下空地继续种植这三种花，经测算需将余下土地面积的 $\text{[math]}$ 种植李花，则李花种植的总面积将达到这三种花种植总面积的 $\text{[math]}$ ．为使桃花种植总面积与樱花种植总面积之比达到 $\text{[math]}$ ，则花园内种植樱花的面积与花园内种植这三种花的总面积之比是．

答案解析收藏纠错 + 选题

三、解答题

19. (2021·北碚模拟)
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2021·北碚模拟) 如图，在四边形ABCD中，AB＝AD，AD//BC
1. （1）在图中，用尺规作线段BD的垂直平分线EF，分别交BD、BC于点E、F.（保留作图痕迹，不写作法）
2. （2）连接DF，证明四边形ABFD为菱形.
答案解析收藏纠错 + 选题

21. (2021·北碚模拟) 某公司在国内有多家门店，共有600名销售人员，为了解该公司各门店销售人员上个月的销售业绩，随机抽取了甲、乙两个门店各30名销售人员在上月的销售数量，并将数据进行整理分析，给出了下面部分信息：

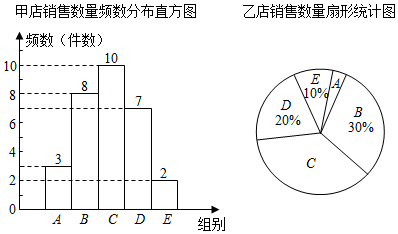
①数据分为五组，分别为A组：x≤40，B组：40＜x≤60，C组：60＜x≤80，D组：80＜x≤100，E组：x＞100；

②样本中甲、乙两门店的最高销售数量都是120件，甲店的最低数量比乙店少两件；

③甲店C组数据：62，69，71，69，78，73，69，79，78，68

乙店C组数据：78，76，69，62，69，71，80，69，73，79，75

④两组数据的平均数、中位数、众数、极差（单位：件）如表所示：

	平均数	中位数	众数	极差
甲店	70	69	69	b
乙店	70	a	69	86

⑤甲店销售数量频数分布直方图和乙店销售数量扇形统计图如下：

（1）扇形统计图A组学生对应的圆心角的度数为，中位数a＝，极差b＝；
（2）通过以上的数据分析，你认为甲、乙两个门店哪个门店的销售人员上月的业绩更好，并说明理由；
（3）若该公司计划将上月销售数量在80件以上（不含80）的员工评为“优秀销售员”，请你估计该公司能评为“优秀销售员”的人数．

答案解析收藏纠错 + 选题

22. (2021·北碚模拟) 有这样一个问题：探究函数y＝ $\text{[math]}$ 的图象与性质，小童根据学习函数的经验，对函数的图象与性质进行例研究，已知当x＝2时，y＝7， $\text{[math]}$ 时，y＝﹣3．下面是小童探究的过程，请补充完整：

（1）该函数的解析式为　　， m＝　　， n＝　　．

根据图中描出的点，画出函数图象．

x	…	﹣4	﹣3	﹣2	0	2	3	4	…
y	…	m	$\text{[math]}$	$\text{[math]}$	﹣3	7	n	$\text{[math]}$	…

（2）根据函图象，下列关于函数性质的描述正确的是；
①该函数图象是中心对称图形，它的对称中心是原点．

②该函数既无最大值也无最小值．

③在自变量的取值范围内，y随x的增大而减小．
（3）请结合（1）中函数图象，直接写出关于x的不等式 $\text{[math]}$ 的解集．（保留1位小数，误差不超过0.2）

答案解析收藏纠错 + 选题

23. (2021·北碚模拟) 为保护人类赖以生存的生态环境，中国植树节定于每年的3月12日，通过立法确定的节日．今年3月某县举办了大型植树活动，现有相邻得A、B两个社区计划共种植78棵，已知A社区每天可以种植6棵树，B社区每天可以种植12棵树．
1. （1）由于人员调动，要求B社区种植天数至少是A社区种植天数的1 $\text{[math]}$ 倍，当种植结束时，A社区至多种植多少天？
2. （2） A、B两个社区种植一棵树的所需费用分别为500元和750元，在（1）问A社区最多种植天数基础上，B社区最少种植了5天．在实际种植过程中，社区决定加大投入，种更多的树，总费用共投入67500元，种植天数比（1）问中A社区最多天数多5a%，B社区每天种植棵树下降a%，种植天数比（1）问中B社区最少种天数多（ $\text{[math]}$ a+30）%，求a的值．
答案解析收藏纠错 + 选题
24. (2021·北碚模拟) 定义：对任意一个三位数a，如果a满足百位数字与十位数字相同，个位数字与十位数字不相同，且都不为零，那么称这个三位数为“半异数”，将一个“半异数”的各个数位上的数字交换后得到新的三位数，把所有的新三位数的和与111的商记为f（a）．例如：a=112，a为“半异数”，将a各个数位上的数字交换后得到新的三位数有121、211、112，所有新三位数的和为121+211+112=444，和与111的商为444÷111=4．所以f（112）=4，根据以上定义，回答下列问题：
1. （1）计算f（227）；
2. （2）数p，q是两个三位数，它们都有“半异数”，p的个位数是3，q的个位数字是5，p≤q．规定 $\text{[math]}$ ，若f （p）+f（q）的和是13的倍数，求k的最大值．
答案解析收藏纠错 + 选题
25. (2021·北碚模拟) 如图1，在平面直角坐标系中，抛物线与x轴交于点A（3，0），B（﹣1，0），与y轴交于C点，且OC＝3OB，连接OD．
1. （1）求抛物线解析式；
2. （2） P点为抛物线上AD部分上一动点，过P点作PF∥DE交AC于F点，求四边形DPAF面积的最大值及此时P点坐标．
3. （3）在（2）问的情况下，把抛物线向右平移两个单位长度，在平面内找一个点N，使以D、P、M、N为顶点的四边形为矩形
答案解析收藏纠错 + 选题
26. (2021·北碚模拟) 如图1，在等腰Rt△ABC中，∠ABC＝90°，AB=BC=6，过点B作BD⊥AC交AC于点D，点E、F分别是线段AB、BC上两点，且BE=BF，连接AF交BD于点Q，过点E作EH⊥AF交AF于点P，交AC于点H．
1. （1）若BF＝4，求△ADQ的面积；
2. （2）求证：CH＝2BQ；
3. （3）如图2，BE＝3，连接EF，将△EBF绕点B在平面内任意旋转，取EF的中点M，连接AM，CM，将线段AM绕点A逆时针旋转90°得线段AN，连接MN、CN，过点N作NR⊥AC交AC于点R，当线段NR的长最小时，直接写出△CMN的周长．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

重庆市北碚区西南大学附中2021年中考数学四模试卷

副标题：

*注意事项：

重庆市北碚区西南大学附中2021年中考数学四模试卷

试题分析

总体分析

题量分析

难度分析

知识点分析