在进行二次根式运算时,形如 一样的式子,我们可以将其进一步化简:
=
=
,以上这种化简的步骤叫做分母有理化.
基本不等式 ≤
(a>0,b>0),当且仅当a=b时等号成立,它是解决最值问题的有力工具.
例如:在x>0的条件下,当x为何值时,x+ 有最小值,最小值是多少?
解:∵x>0, >0∴
≥
,即
≥2
,∴
≥2
当且仅当x= ,即x=1时,x+
有最小值,最小值为2.
请根据阅读材料解答下列问题:
材料一:平方运算和开方运算是互逆运算.如a2±2ab+b2=(a±b)2 , 那么 ,如何将双重二次根式
化简.我们可以把
转化为
完全平方的形式,因此双重二次根式
得以化简.
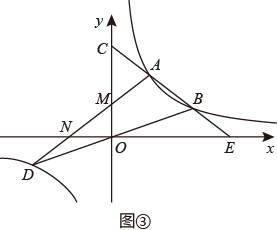
材料二:在直角坐标系xOy中,对于点P(x,y)和Q(x,y’)给出如下定义:若 则称点Q为点P的“横负纵变点”.例如:点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5).问题:
细心观察图形,认真分析下列各式,然后解答问题:

( )2+1=2,S1=
;(
)2+1=3,S2=
;(
)2+1=4,S3=
;….
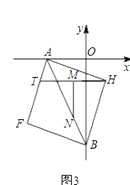
以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时, 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.