 B .
B .  C .
C .  D .
D . 
| 一天加工该工件的个数(个) | 70 | 80 | 90 | 100 | 110 |
| 工人人数 | 4 | 11 | 10 | 8 | 7 |

![]()
|
地点 |
票价 |
|
历史博物馆 |
10元 |
| 民俗展览馆 | 20元 |


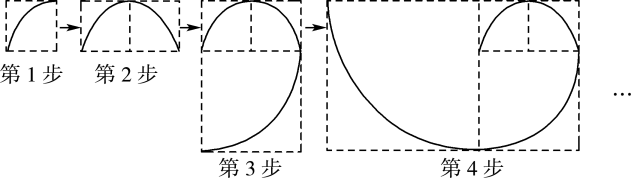
①图象G对应的函数y的值随x的增大而 ▲ (填“增大”或“减小”),自变量x的取值范围为 ▲ ;
②求图象G最高点的坐标.

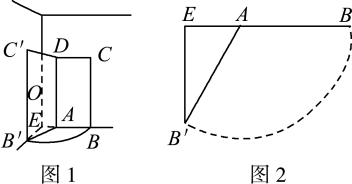
①如图2,在等边中,
, 点D,E分别在
上,
, 当
的长为时,四边形
为“等邻对角四边形”.
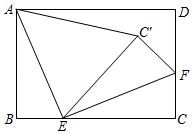
②如图3,在中,点E,D在
上,点F在
上,
, 四边形
为“等邻对角四边形”,若
, 则
的度数为.
根据图1及其条件,探究与
的数量关系.
如图4,在“等邻对角四边形”中,
与
的延长线相交于点E.若
, 求
的长,并指出
的度数是否可以等于90°,不必说明理由.