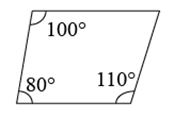
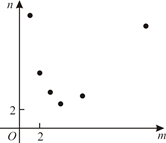
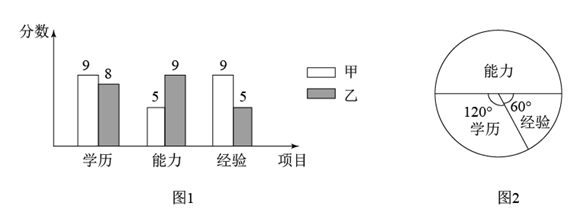
 B .
B . 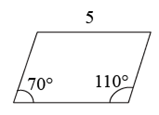 C .
C . 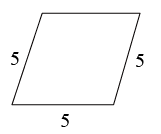 D .
D . 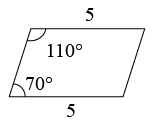
 B .
B . 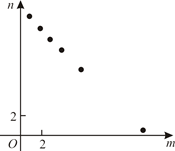 C .
C . 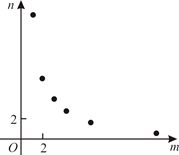 D .
D . 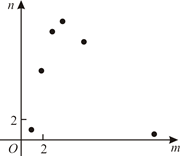
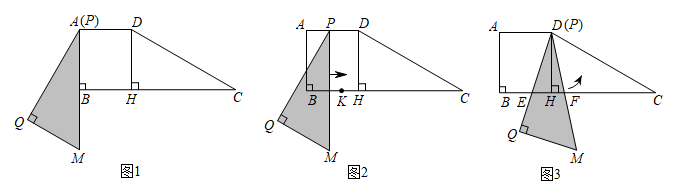
①边PQ从平移开始,到绕点D旋转结束,求边PQ扫过的面积;
②如图2,点K在BH上,且 .若△PQM右移的速度为每秒1个单位长,绕点D旋转的速度为每秒5°,求点K在△PQM区域(含边界)内的时长;
③如图3.在△PQM旋转过程中,设PQ , PM分别交BC于点E , F , 若BE=d , 直接写出CF的长(用含d的式子表示).