 B .
B .  C .
C .  D .
D . 
①汽车从A地匀速行驶到B地,汽车的剩余路程y与行驶时间x;②将水箱中的水匀速放出,直至放完,水箱中的剩余水量y与放水时间x;③用长度一定的绳子围成一个矩形,矩形的面积y与一边长x,其中,变量y与变量x之间的函数关系可以利用如图所示的图象表示的是( )

鞋号 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 |
销售量/双 | 2 | 4 | 5 | 5 | 12 | 6 | 3 | 2 | 1 |
根据以上数据,估计该商场进鞋号需求最多的滑冰鞋的数量为双.
包裹编号 | I号产品重量/吨 | II号产品重量/吨 | 包裹的重量/吨 |
A | 5 | 1 | 6 |
B | 3 | 2 | 5 |
C | 2 | 3 | 5 |
D | 4 | 3 | 7 |
E | 3 | 5 | 8 |
甲工厂准备用一辆载重不超过19.5吨的货车将部分包裹一次运送到乙工厂.
已知:如图, 求证: | |
方法一 证明:如图,过点A作
| 方法二 证明:如图,过点C作 |
a.甲、乙两位同学得分的折线图:
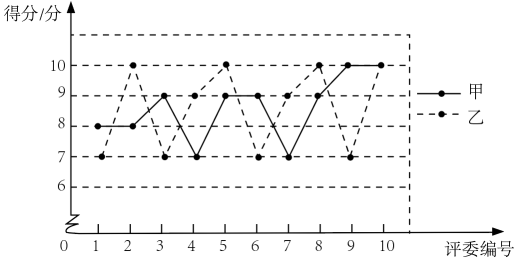
b.丙同学得分:
10,10,10,9,9,8,3,9,8,10
c.甲、乙、丙三位同学得分的平均数:
同学 | 甲 | 乙 | 丙 |
平均数 | 8.6 | 8.6 | m |
根据以上信息,回答下列问题:
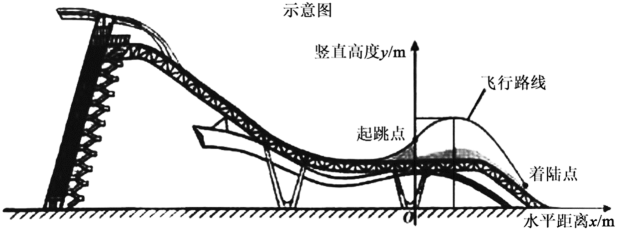
某运动员进行了两次训练.
水平距离x/m | 0 | 2 | 5 | 8 | 11 | 14 |
竖直高度y/m | 20.00 | 21.40 | 22.75 | 23.20 | 22.75 | 21.40 |
根据上述数据,直接写出该运动员竖直高度的最大值,并求出满足的函数关系
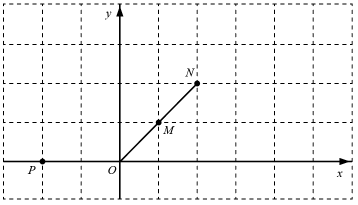
①在图中画出点;
②连接交线段
于点
求证: