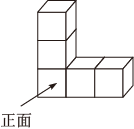
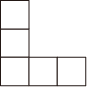
 B .
B . 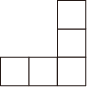

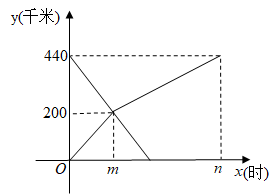
根据以上信息回答下列问题:
①因为2019年的专利授权量年增长率最低,所以2019年的专利授权量的增长量就最小.()
②与2018年相比,2019年的专利授权量年增长率虽然下降,但专利授权量仍然上升.这是因为专利授权量年增长率 , 所以只要专利授权量年增长率大于零,当年专利授权量就一定增加.()
③通过统计数据,可以看出长春市区域科技创新力呈上升趋势,为国家科技自立自强贡献吉林力量.()
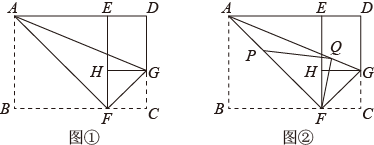
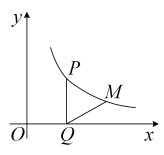
小亮对上面的猜想进行了证明,下面是部分证明过程:
证明:四边形是矩形,
∴ .
由折叠可知, ,
.
∴ .
∴ .
请你补全余下的证明过程.
的度数为度,
的值为;