 B .
B . 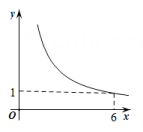 C .
C .  D .
D . 

① ;②
;③
;④
;⑤
.
其中正确的是( )


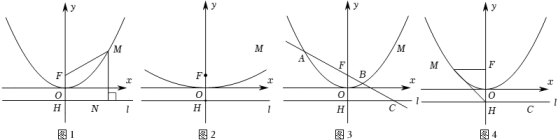
请分别直接写出抛物线y=2x2的焦点坐标和准线l的方程:,.
如图2所示,已知抛物线y=x2上一点P到准线l的距离为6,求点P的坐标;
如图3所示,已知过抛物线y=ax2(a>0)的焦点F的直线依次交抛物线及准线l于点A、B、C.若BC=2BF,AF=4,求a的值;
古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点C将一条线段AB分为两段AC和CB,使得其中较长一段AC是全线段AB与另一段CB的比例中项,即满足:=
=
.后人把
这个数称为“黄金分割”把点C称为线段AB的黄金分割点.
如图4所示,抛物线y=x2的焦点F(0,1),准线l与y轴交于点H(0,﹣1),E为线段HF的黄金分割点,点M为y轴左侧的抛物线上一点.当
=
时,请直接写出△HME的面积值.
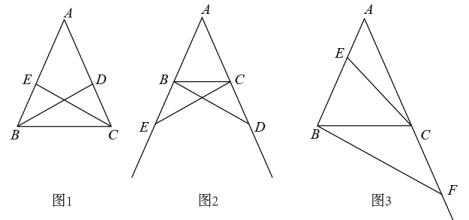
①BD,CE是△ABC的角平分线.求证:BD=CE.
②点D,E分别是边AC,AB的中点,连接BD,CE.求证:BD=CE.
(从①②两题中选择一题加以证明)
经过做题反思,小明同学认为:在△ABC中,AB=AC,D为边AC上一动点(不与点A,C重合).对于点D在边AC上的任意位置,在另一边AB上总能找到一个与其对应的点E,使得BD=CE.进而提出问题:若点D,E分别运动到边AC,AB的延长线上,BD与CE还相等吗?请解决下面的问题:
如图2,在△ABC中,AB=AC,点D,E分别在边AC,AB的延长线上,请添加一个条件(不再添加新的字母),使得BD=CE,并证明.
如图3,在△ABC中,AB=AC=2,∠A=36°,E为边AB上任意一点(不与点A,B重合),F为边AC延长线上一点.判断BF与CE能否相等.若能,求CF的取值范围;若不能,说明理由.