 B .
B .  C .
C .  D .
D . 
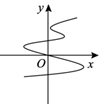 B .
B . 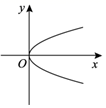 C .
C . 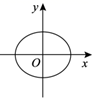 D .
D . 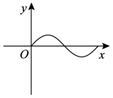
 B .
B .  C .
C .  D .
D . 
甲 | 乙 | 丙 | 丁 | |
平均数 | 181 | 183 | 183 | 181 |
方差 | 1.6 | 3.4 | 1.6 | 3.4 |
要选择一名成绩好且发挥稳定的同学参加比赛,应该选择( )
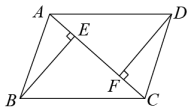
在数学课上,老师提出如下问题:
已知:如图,在 求作:矩形
|
小明的思考过程是:
①由于求作矩形,回顾了矩形的定义和判定: 矩形的定义:有一个角是直角的平行四边形叫做矩形; 矩形判定1:对角线相等的平行四边形是矩形; 矩形判定2:有三个角是直角的四边形是矩形. ②条件给出了 ③小明决定通过作线段AC的垂直平分线,作出线段 |
小明的作法如下:
作法:①分别以点A,C为圆心,大于 ③作直线 ③作射线 ④连接 ∴ 四边形
|
请你根据小明同学设计的尺规作图过程:
证明:∵直线是
的垂直平分线,
∴ ,
∵ ,
∴四边形是平行四边形( ① )(填推理的依据).
∵ ,
∴四边形是矩形( ② )(填推理的依据).
(温馨提示:保留作图痕迹,不用写作法和证明)


a.50名学生的测试分数(百分制)如下:
77 79 80 60 85 66 86 87 68 89
91 82 68 85 65 82 57 66 86 87
69 67 79 79 86 79 87 89 90 89
81 80 72 82 84 82 65 76 76 97
98 55 89 70 71 78 59 52 70 60
b.按如下分组整理、描述样本数据:
成绩x(单位:分) | 频数 | 频率 |
4 | 0.08 | |
a | 0.20 | |
12 | b | |
20 | 0.40 | |
4 | 0.08 | |
合计 | 50 | 1.00 |

请根据以上信息,解答下列问题:
①如果矩形的面积小于6,求m的取值范围;
②直线(
)与直线
交于点E,
, 直接写出点E的坐标.
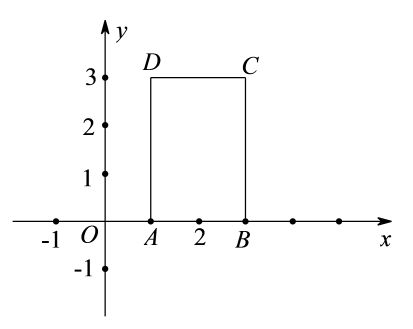
直线关于矩形
的“截距”是
, 求m的值.