2023年中考数学复习考点一遍过——函数基础知识

更新时间：2022-12-25 浏览次数：123 类型：一轮复习

一、单选题（每题3分，共30分）

1. (2024八下·任丘期末) 水中涟漪（圆形水波）不断扩大，记它的半径为r，则圆周长C与r的关系式为 $\text{[math]}$ ．下列判断正确的是（）

A . 2是变量 B . $\text{[math]}$ 是变量 C . r是变量 D . C是常量

答案解析收藏纠错 + 选题
2. (2024九下·枣庄模拟) 函数 $\text{[math]}$ 的自变量x的取值范围是（）

A . $\text{[math]}$ 且 $\text{[math]}$ B . $\text{[math]}$ 且 $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 且 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九下·花溪模拟) 某城市市区人口 $\text{[math]}$ 万人，市区绿地面积50万平方米，平均每人拥有绿地 $\text{[math]}$ 平方米，则 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数表达式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022·乐山) 点 $\text{[math]}$ 所在象限是（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
5. (2024八上·乌当期末) 甲、乙两人沿同一直道从 $\text{[math]}$ 地到 $\text{[math]}$ 地，在整个行程中，甲、乙离 $\text{[math]}$ 地的距离 $\text{[math]}$ 与时间 $\text{[math]}$ 之间的函数关系如图所示，下列说法错误的是（）

A . 甲比乙早1分钟出发 B . 乙的速度是甲的速度的2倍 C . 若甲比乙晚5分钟到达，则甲用时10分钟 D . 若甲出发时的速度为原来的2倍，则甲比乙提前1分钟到达 $\text{[math]}$ 地

答案解析收藏纠错 + 选题
6. (2022·黄石) 如图，正方形 $\text{[math]}$ 的边长为 $\text{[math]}$ ，将正方形 $\text{[math]}$ 绕原点O顺时针旋转45°，则点B的对应点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·枣庄) 已知y₁和y₂均是以x为自变量的函数，当x＝n时，函数值分别是N₁和N₂ ，若存在实数n，使得N₁+N₂＝1，则称函数y₁和y₂是“和谐函数”．则下列函数y₁和y₂不是“和谐函数”的是（）

A . y₁＝x²+2x和y₂＝﹣x+1 B . y₁＝ $\text{[math]}$ 和y₂＝x+1 C . y₁＝﹣ $\text{[math]}$ 和y₂＝﹣x﹣1 D . y₁＝x²+2x和y₂＝﹣x﹣1

答案解析收藏纠错 + 选题
8. (2022·河池) 东东用仪器匀速向如图容器中注水，直到注满为止.用t表示注水时间，y表示水面的高度，下列图象适合表示y与t的对应关系的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2022·宜昌) 如图是一个教室平面示意图，我们把小刚的座位“第1列第3排”记为 $\text{[math]}$ .若小丽的座位为 $\text{[math]}$ ，以下四个座位中，与小丽相邻且能比较方便地讨论交流的同学的座位是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022·随州) 已知张强家、体育场、文具店在同一直线上.下面的图象反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后又走到文具店去买笔，然后散步走回家.图中x表示时间，y表示张强离家的距离.则下列结论不正确的是（）

A . 张强从家到体育场用了15min B . 体育场离文具店1.5km C . 张强在文具店停留了20min D . 张强从文具店回家用了35min

答案解析收藏纠错 + 选题

二、填空题（每空3分，共30分）

11. (2022·青海) 若式子 $\text{[math]}$ 有意义，则实数x的取值范围是.

答案解析收藏纠错 + 选题
12. (2022·广安) 若点P（m+1，m）在第四象限，则点Q（﹣3，m+2）在第象限.

答案解析收藏纠错 + 选题
13. (2022·贺州) 如图，在平面直角坐标系中， $\text{[math]}$ 为等腰三角形， $\text{[math]}$ ，点B到x轴的距离为4，若将 $\text{[math]}$ 绕点O逆时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为.

答案解析收藏纠错 + 选题
14. (2022·鄂州) 中国象棋文化历史久远.某校开展了以“纵横之间有智意攻防转换有乐趣”为主题的中国象棋文化节，如图所示是某次对弈的残局图，如果建立平面直角坐标系，使“帥”位于点（﹣1，﹣2），“馬”位于点（2，﹣2），那么“兵”在同一坐标系下的坐标是.

答案解析收藏纠错 + 选题
15. 如图，在平面直角坐标系中，把一个点从原点开始向上平移1个单位，再向右平移1个单位，得到点 $\text{[math]}$ ；把点 $\text{[math]}$ 向上平移2个单位，再向左平移2个单位，得到点 $\text{[math]}$ ；把点 $\text{[math]}$ 向下平移3个单位，再向左平移3个单位，得到点 $\text{[math]}$ ；把点 $\text{[math]}$ 向下平移4个单位，再向右平移4个单位，得到点 $\text{[math]}$ ；…；按此做法进行下去，则点 $\text{[math]}$ 的坐标为.

答案解析收藏纠错 + 选题
16. (2022·丽水) 三个能够重合的正六边形的位置如图.已知B点的坐标是（﹣ $\text{[math]}$ ，3），则A点的坐标是

答案解析收藏纠错 + 选题
17. (2023九下·孝南月考) 函数 $\text{[math]}$ 的自变量 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
18. (2022·舟山) 某动物园利用杠杆原理称象；如图，在点P处挂一根质地均匀且足够长的钢梁(呈水平状态)，将装有大象的铁笼和弹簧秤(秤的重力忽略不许)分别悬挂在钢梁的点A、B处，当钢梁保持水平时，弹簧秤读数为k(N)，若铁笼固定不动，移动弹簧秤使BP扩大到原来的n(n>1)倍，且钢梁保持水平，则弹簧秤读数为(N)(用含n，k的代数式表示)

答案解析收藏纠错 + 选题
19. (2022·孝感) 如图1，在△ABC中，∠B＝36°，动点P从点A出发，沿折线A→B→C匀速运动至点C停止.若点P的运动速度为1cm/s，设点P的运动时间为t（s），AP的长度为y（cm），y与t的函数图象如图2所示.当AP恰好平分∠BAC时，t的值为.

答案解析收藏纠错 + 选题
20. (2024八上·梅县区期末) 一个装有进水管和出水管的容器，开始时，先打开进水管注水，3分钟时，再打开出水管排水，8分钟时，关闭进水管，直至容器中的水全部排完.在整个过程中，容器中的水量y（升）与时间x（分钟）之间的函数关系如图所示，则图中a的值为.

答案解析收藏纠错 + 选题

三、综合题（共6题，共60分）

21. (2023·大安模拟) 已知A、B两地之间有一条长440千米的高速公路．甲、乙两车分别从A、B两地同时出发，沿此公路相向而行，甲车先以100千米/时的速度匀速行驶200千米后与乙车相遇，再以另一速度继续匀速行驶4小时到达B地；乙车匀速行驶至A地，两车到达各自的目的地后停止．两车距A地的路程y（千米）与各自的行驶时间x（时）之间的函数关系如图所示．
1. （1） m=，n=；
2. （2）求两车相遇后，甲车距A地的路程y与x之间的函数关系式；
3. （3）当乙车到达A地时，求甲车距A地的路程．
答案解析收藏纠错 + 选题
22. (2024·宣恩模拟) 某超市销售一种进价为18元/千克的商品，经市场调查后发现，每天的销售量y（千克）与销售单价x（元/千克）有如下表所示的关系：
销售单价x（元/千克）
…
20
22.5
25
37.5
40
…
销售量y（千克）
…
30
27.5
25
12.5
10
…
1. （1）根据表中的数据在下图中描点 $\text{[math]}$ ，并用平滑曲线连接这些点，请用所学知识求出y关于x的函数关系式；
2. （2）设该超市每天销售这种商品的利润为w（元）（不计其它成本），
  ①求出w关于x的函数关系式，并求出获得最大利润时，销售单价为多少；
  ②超市本着“尽量让顾客享受实惠”的销售原则，求 $\text{[math]}$ （元）时的销售单价.
答案解析收藏纠错 + 选题
23. (2022·常州) 如图，点 $\text{[math]}$ 在射线 $\text{[math]}$ 上， $\text{[math]}$ .如果 $\text{[math]}$ 绕点 $\text{[math]}$ 按逆时针方向旋转 $\text{[math]}$ 到 $\text{[math]}$ ，那么点 $\text{[math]}$ 的位置可以用 $\text{[math]}$ 表示.
1. （1）按上述表示方法，若 $\text{[math]}$ ， $\text{[math]}$ ，则点 $\text{[math]}$ 的位置可以表示为；
2. （2）在（1）的条件下，已知点 $\text{[math]}$ 的位置用 $\text{[math]}$ 表示，连接 $\text{[math]}$ 、 $\text{[math]}$ .求证： $\text{[math]}$ .
答案解析收藏纠错 + 选题
24. (2022·天津) 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．
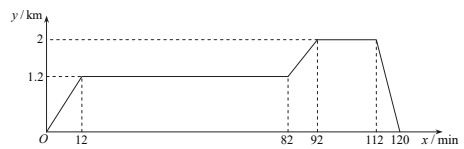
已知学生公寓、阅览室、超市依次在同一条直线上，阅览室离学生公寓 $\text{[math]}$ ，超市离学生公寓 $\text{[math]}$ ，小琪从学生公寓出发，匀速步行了 $\text{[math]}$ 到阅览室；在阅览室停留 $\text{[math]}$ 后，匀速步行了 $\text{[math]}$ 到超市；在超市停留 $\text{[math]}$ 后，匀速骑行了 $\text{[math]}$ 返回学生公寓．给出的图象反映了这个过程中小琪离学生公寓的距离 $\text{[math]}$ 与离开学生公寓的时间 $\text{[math]}$ 之间的对应关系．
请根据相关信息，解答下列问题：
1. （1）填表：
  离开学生公寓的时间/ $\text{[math]}$
  5
  8
  50
  87
  112
  离学生公寓的距离/ $\text{[math]}$
  0.5
  1.6
2. （2）填空：
  ①阅览室到超市的距离为 $\text{[math]}$ ；
  ②小琪从超市返回学生公寓的速度为 $\text{[math]}$ ；
  ③当小琪离学生公寓的距离为 $\text{[math]}$ 时，他离开学生公寓的时间为 $\text{[math]}$ ．
3. （3）当 $\text{[math]}$ 时，请直接写出y关于x的函数解析式．
答案解析收藏纠错 + 选题

25. (2023·铜川模拟) 如图，是一个“函数求值机”的示意图，其中y是x的函数.下面表格中，是通过该“函数求值机”得到的几组x与y的对应值.

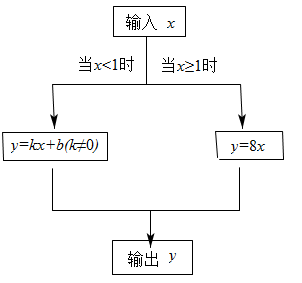
输人x	…	-6	-4	-2	0	2	…
输出y	…	-6	-2	2	6	16	…

根据以上信息，解答下列问题：

（1）当输入的x值为1时，输出的y值为；
（2）求k，b的值；
（3）当输出的y值为0时，求输入的x值.

答案解析收藏纠错 + 选题

26. (2022·嘉兴) 6月13日，某港口的湖水高度y（cm）和时间x（h）的部分数据及函数图象如下：

x(h)	…	11	12	13	14	15	16	17	18	…
Y(cm	…	189	137	103	80	101	133	202	260	…

（数据来自某海洋研究所）

（1）数学活动：
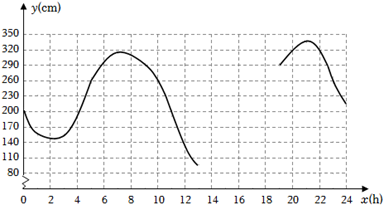
①根据表中数据，通过描点、连线（光滑曲线）的方式补全该函数的图象．

②观察函数图象，当x＝4时，y的值为多少？当y的值最大时，x的值为多少？
（2）数学思考：
请结合函数图象，写出该函数的两条性质或结论．
（3）数学应用：
根据研究，当潮水高度超过260cm时，货轮能够安全进出该港口.请问当天什么时间段适合货轮进出此港口？

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

2023年中考数学复习考点一遍过——函数基础知识

副标题：

*注意事项：

2023年中考数学复习考点一遍过——函数基础知识

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

销售单价x（元/千克）	…	20	22.5	25	37.5	40	…
销售量y（千克）	…	30	27.5	25	12.5	10	…

离开学生公寓的时间/ $\text{[math]}$	5	8	50	87	112
离学生公寓的距离/ $\text{[math]}$	0.5			1.6