浙教版备考2023年中考数学一轮复习41.二次函数与不等式（...

更新时间：2022-12-31 浏览次数：65 类型：一轮复习

一、单选题（每题3分，共30分）

1. (2022九上·霍邱月考) 一次函数y₁=mx+n(m≠0)与二次函数y₂=ax²+bx+c(a≠0)的图象如图所示，则不等式ax²+bx+c>mx+n的解集为（）

A . -4<x<3 B . x<-4 C . 3-<<x<-4 D . x>3或x<-4

答案解析收藏纠错 + 选题
2. (2022·台儿庄模拟) 如图，已知抛物线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点，则关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 的解集是（）

A . $\text{[math]}$ 或 $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022九上·舟山期中) 在研究函数图形的性质时，若将自变量x变为 $\text{[math]}$ ，则函数图象变化为：保留y轴右侧的图象，y轴左侧的图像变为右侧图象关于y轴的对称图形．已知抛物线y＝-x2+2x＋3的图象，则对于 $\text{[math]}$ ，当y＞0时，x的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022九上·滁州期中) 如图，抛物线 $\text{[math]}$ 关于直线 $\text{[math]}$ 对称，点 $\text{[math]}$ 在抛物线上，那么使得 $\text{[math]}$ 的x的取值范围是（）

A . $\text{[math]}$ 或 $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022九上·上城期中) 如图，二次函数 $\text{[math]}$ 的图象的对称轴为x＝ $\text{[math]}$ ，且经过点（﹣2，0），（ $\text{[math]}$ ），（ $\text{[math]}$ ），下列说法正确的是（　　）

A . bc＞0 B . 当 $\text{[math]}$ ≥﹣ $\text{[math]}$ 时， $\text{[math]}$ C . a＝2b D . 不等式 $\text{[math]}$ 的解集是﹣2＜x＜ $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·临清模拟) 已知抛物线 $\text{[math]}$ （ $\text{[math]}$ ）与直线 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点，则关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 的解集是（）

A . $\text{[math]}$ 或 $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021九上·东莞期末) 如图，二次函数y＝ax²+bx+c与反比例函数y＝ $\text{[math]}$ 的图象相交于点A（﹣1，y₁）、B（1，y₂）、C（3，y₃）三个点，则不等式ax²+bx+c＞ $\text{[math]}$ 的解集是（）

A . ﹣1＜x＜0或1＜x＜3 B . x＜﹣1或1＜x＜3 C . ﹣1＜x＜0或x＞3 D . ﹣1＜x＜0或0＜x＜1

答案解析收藏纠错 + 选题
8. (2021·鹿城模拟) 在平面直角坐标系中，点 $\text{[math]}$ ， $\text{[math]}$ 的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ，若抛物线 $\text{[math]}$ 与线段 $\text{[math]}$ 有且只有一个交点，则 $\text{[math]}$ 的值可以是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022·内江) 如图，抛物线y＝ax²+bx+c与x轴交于两点（x₁ ， 0）、（2，0），其中0＜x₁＜1.下列四个结论：①abc＜0；②a+b+c＞0；③2a﹣c＞0；④不等式ax²+bx+c＞﹣ $\text{[math]}$ x+c的解集为0＜x＜x₁.其中正确结论的个数是（）

A . 4 B . 3 C . 2 D . 1

答案解析收藏纠错 + 选题
10. (2024九下·金山月考) 已知 $\text{[math]}$ ， $\text{[math]}$ 为抛物线 $\text{[math]}$ 图象上的两点，且 $\text{[math]}$ ，则下列说法正确的是（）

A . 若 $\text{[math]}$ ，则 $\text{[math]}$ B . 若 $\text{[math]}$ ，则 $\text{[math]}$ C . 若 $\text{[math]}$ ，则 $\text{[math]}$ D . 若 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每题4分，共24分）

11. (2022九上·义乌期中) 如图，直线y＝kx+b与抛物线y＝-x²+2x+3交于点A，B，且点A在y轴上，点B在x轴上，则不等式-x²+2x+3＞kx+b的解集为．

答案解析收藏纠错 + 选题
12. (2022九上·龙口期中) 如图抛物线y=ax²与反比例函数 $\text{[math]}$ 交于点C（1，2），不等式 $\text{[math]}$ 的解集是．

答案解析收藏纠错 + 选题
13. (2022九下·蓬安开学考) 如图，已知抛物线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于 $\text{[math]}$ 两点，则关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 的解集是.

答案解析收藏纠错 + 选题
14. (2022·朝阳模拟) 抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ， $\text{[math]}$ 两点，则不等式 $\text{[math]}$ 的解集是.

答案解析收藏纠错 + 选题
15. (2021·淮安模拟) 抛物线y=ax²+bx+c的部分图象如图所示，则不等式ax²+bx+c＞0的解集为.

答案解析收藏纠错 + 选题
16. (2020九上·宜春期中) 已知抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴分别交于点 $\text{[math]}$ 和 $\text{[math]}$ ，则不等式 $\text{[math]}$ 的解集为．

答案解析收藏纠错 + 选题

三、解答题（共7题，共66分）

17. (2022九下·鄂州月考) 自主学习，请阅读下列解题过程.
解一元二次不等式：x²﹣5x＞0

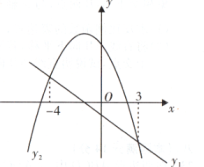
解：设x²﹣5x=0，解得x₁=0，x₂=5，则抛物线y=x²﹣5x与x轴的交点坐标为（0，0）和（5，0）.画出二次函数y=x²﹣5x的大致图象（如图所示），由图象可知：当x＜0，或x＞5时函数图象位于x轴上方，此时y＞0，即x²﹣5x＞0，所以，一元二次不等式x²﹣5x＞0的解集为：x＜0或x＞5.

通过对上述解题过程的学习，按其解题的思路和方法解答下列问题：
1. （1）一元二次不等式x²﹣5x＜0的解集为.
2. （2）用类似的方法解一元二次不等式：x²﹣2x﹣3＞0.
答案解析收藏纠错 + 选题
18. (2022九上·海淀期中) 在平面直角坐标系xOy中，二次函数 $\text{[math]}$ 图象顶点为A，与x轴正半轴交于点B．
1. （1）求点B的坐标，并画出这个二次函数的图象；
2. （2）一次函数 $\text{[math]}$ 的图象过A，B两点，结合图象，直接写出关于x的不等式 $\text{[math]}$ 的解集．
答案解析收藏纠错 + 选题
19. (2021九上·南阳月考) 抛物线 $\text{[math]}$ 的图象如图所示，根据图象回答问题.
1. （1）直接写出 $\text{[math]}$ 时， $\text{[math]}$ 随 $\text{[math]}$ 的增大而；
2. （2）直接写出方程 $\text{[math]}$ 的根；
3. （3）直接写出不等式 $\text{[math]}$ 的解集；
4. （4）若方程 $\text{[math]}$ 没有实数根，直接写出 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
20. (2021九上·德州期中) 如图，二次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ 在抛物线上，且与点 $\text{[math]}$ 关于抛物线的对称轴对称，已知一次函数 $\text{[math]}$ 的图象经过该二次函数图象上的点 $\text{[math]}$ 及点 $\text{[math]}$ ．
1. （1）求二次函数和点 $\text{[math]}$ 的坐标；
2. （2）根据图象，写出满足 $\text{[math]}$ 的 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
21. (2022九下·杭州月考) 在平面直角坐标系内，设二次函数y₁＝(x－a)²＋a－1(a为常数)．
1. （1）若函数y₁的图象经过点(1，2)，求函数y₁的表达式．
2. （2）若函数y₁的图象与一次函数y₂＝x＋b(b为常数)的图象有且仅有一个交点，求b 的值．
3. （3）已知(m，n)( m＞0)在函数y₁的图象上，当m＞2a时，求证：n＞．
答案解析收藏纠错 + 选题
22. (2021九上·嘉兴期中) 某商场经营某种品牌的玩具，购进时的单价是30元，根据市场调查：在一段时间内，销售单价是40元时，销售量是600件，而销售单价每涨1元，就会少售出10件玩具。
1. （1）不妨设该种品牌玩具的销售单价为在40元的基础上上涨x（x＞0），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润W（元），并把结果填写在表格中：
  
  销售单价（元）
  
  40+x
  
  销售量y（件）
  
  销售玩具获得利润W（元）
2. （2）在（1）问条件下，若商场获得10000元销售利润，则该玩具销售单价应定为多少元？
3. （3）在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于44元，且商场要完成不少于540件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？
答案解析收藏纠错 + 选题
23. (2023九上·钱江月考) 已知关于 $\text{[math]}$ 的函数 $\text{[math]}$ .
1. （1）若 $\text{[math]}$ ，函数的图象经过点 $\text{[math]}$ 和点 $\text{[math]}$ ，求该函数的表达式和最小值；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 时，函数的图象与 $\text{[math]}$ 轴有交点，求 $\text{[math]}$ 的取值范围.
3. （3）阅读下面材料：
  设 $\text{[math]}$ ，函数图象与 $\text{[math]}$ 轴有两个不同的交点 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ 两点均在原点左侧，探究系数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 应满足的条件，根据函数图象，思考以下三个方面：
  
  ①因为函数的图象与 $\text{[math]}$ 轴有两个不同的交点，所以 $\text{[math]}$ ；
  
  ②因为 $\text{[math]}$ ， $\text{[math]}$ 两点在原点左侧，所以 $\text{[math]}$ 对应图象上的点在 $\text{[math]}$ 轴上方，即 $\text{[math]}$ ；
  
  ③上述两个条件还不能确保 $\text{[math]}$ ， $\text{[math]}$ 两点均在原点左侧，我们可以通过抛物线的对称轴位置来进一步限制抛物线的位置：即需 $\text{[math]}$ .
  
  综上所述，系数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 应满足的条件可归纳为： $\text{[math]}$
  
  请根据上面阅读材料，类比解决下面问题：
  
  若函数 $\text{[math]}$ 的图象在直线 $\text{[math]}$ 的右侧与 $\text{[math]}$ 轴有且只有一个交点，求 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题