2022-2023学年苏科版数学八年级上学期期末练习卷3

更新时间：2023-01-04 浏览次数：111 类型：期末考试

一、单选题（每题2分，共16分）

1. (2021八上·泰州期末) 下列各组数中是勾股数的是（）

A . 4，5， 6 B . 1.5，2， 2.5 C . 11，60， 61 D . 1， $\text{[math]}$ ，2

答案解析收藏纠错 + 选题
2. (2021八上·桓台期末) 下列图形中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022八上·海曙期中) 如图，用三角尺可按下面方法画角平分线：在已知的∠AOB 的两边上分别取点M、N，使OM＝ON，再分别过点M、N作OA、OB的垂线，交点为P，画射线OP．可证得△POM≌△PON，OP平分∠AOB．以上依画法证明△POM≌△PON根据的是（）

A . SSS B . SAS C . AAS D . HL

答案解析收藏纠错 + 选题
4. (2024七下·吉林期中) 若点A(-2，n)在x轴上，则点B(n-1，n+1)在（）.

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
5. (2024八下·新田月考) 如图，台阶阶梯每一层高20cm，宽30cm，长50cm，一只蚂蚁从A点爬到B点，最短路程是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 120 D . 130

答案解析收藏纠错 + 选题
6. (2021八下·西宁期中) 如图，在正方形ABCD中，E是AB上一点，BE=2，AE=3BE，P是AC上一动点，则PB+PE的最小值为（）.

A . 8 $\text{[math]}$ B . 8 C . 10 D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022八下·赵县期末) 在同一直角坐标系中，一次函数y＝（k﹣2）x+k的图象与正比例函数y＝kx图象的位置可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2021八上·瑶海期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是边 $\text{[math]}$ 上的两点，且 $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 之间的关系式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每题2分，共20分）

9. (2021八下·乐清期末) 当x= 时， $\text{[math]}$ 值为0。

答案解析收藏纠错 + 选题
10. (2019八下·梁子湖期中) 如图，数轴上点A表示数－1，点B表示数1，过点B作BC垂直于数轴，若BC＝1，以A为圆心，AC为半径作圆弧交数轴的正半轴于点P，则点P所表示的数是 .

答案解析收藏纠错 + 选题
11. (2020八下·泰兴期中) 为了比较 $\text{[math]}$ +1与 $\text{[math]}$ 的大小，可以构造如图所示的图形进行推算，其中∠C＝90°，BC＝4，D在BC上且BD＝AC＝1.通过计算可得 $\text{[math]}$ +1 $\text{[math]}$ .（填“＞”或“＜”或“＝”）

答案解析收藏纠错 + 选题
12. (2021八上·绵阳期中) 如图， $\text{[math]}$ ABC中，AC=BC，且点D在 $\text{[math]}$ ABC外，D在AC的垂直平分线上，连接BD，若∠DBC=30°∠ACD=13°，则∠A=°

答案解析收藏纠错 + 选题
13. (2023八下·无棣期末) 把直线y= $\text{[math]}$ x+1向右平移个单位可得到直线y= $\text{[math]}$ x-2．

答案解析收藏纠错 + 选题
14. (2020八下·呼和浩特月考) 如图，函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象交于 $\text{[math]}$ ．则不等式 $\text{[math]}$ 的解集为．

答案解析收藏纠错 + 选题
15. (2021八上·瑞安期末) 一条笔直的公路上依次有A，B，C三地，甲，乙两人同时从A地出发，甲先使用共享单车，经过B地到达停车点C地后再步行返回B地，此时直接步行的乙也恰好到达B地.已知两人步行速度相同，两人离起点A的距离y（米）关于时间x（分）的函数关系如图，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2020八下·西安月考) 如图，已知正方形ABOC的顶点B(2，1)，则顶点C的坐标为．

答案解析收藏纠错 + 选题
17. (2020八下·禹城期末) 已知一次函数 $\text{[math]}$ 为常数），当x＜2时，y＞0，则 $\text{[math]}$ 的取值范围为．

答案解析收藏纠错 + 选题
18. (2022八下·北仑期末) 如图，正方形ABCD边长为2，F为对角线AC上的一个动点，过C作AC的垂线并截取 $\text{[math]}$ ，连结EF， $\text{[math]}$ 周长的最小值为．

答案解析收藏纠错 + 选题

三、解答题（共9题，共64分）

19. (2024七下·霍城期中) 求下列各式中x的值：
1. （1） 2x²－32＝0；
2. （2） (x＋4)³＋64＝0.
答案解析收藏纠错 + 选题
20. (2021八下·华坪期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是对角线， $\text{[math]}$ ⊥ $\text{[math]}$ ， $\text{[math]}$ ⊥ $\text{[math]}$ ，垂足分别为E、F．求证：△ $\text{[math]}$ ≌△ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2020八上·泰兴月考) 作图题
1. （1）如图所示，画出△ABC关于直线MN的轴对称图形.
2. （2）已知：∠AOB和两点M、N，求作：一点P，使点P到∠AOB两边的距离相等，且PM＝PN.（尺规作图，保留作图痕迹）
答案解析收藏纠错 + 选题
22. (2022八下·永定期末) 明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，踏板一尺离地，送行二步恰竿齐，五尺板高离地…”翻译成现代文为：如图，秋千 $\text{[math]}$ 静止的时候，踏板离地高一尺（ $\text{[math]}$ 尺），将它往前推进两步（ $\text{[math]}$ 尺），此时踏板升高离地五尺（ $\text{[math]}$ 尺），求秋千绳索（ $\text{[math]}$ 或 $\text{[math]}$ ）的长度．

答案解析收藏纠错 + 选题
23. (2021八下·古冶期末) 已知y是x的一次函数，且当 $\text{[math]}$ 时， $\text{[math]}$ ；当 $\text{[math]}$ 时， $\text{[math]}$ ．
1. （1）求这个一次函数的解析式；
2. （2）当 $\text{[math]}$ 时，求函数y的值；
3. （3）当 $\text{[math]}$ 时，求自变量x的取值范围．
答案解析收藏纠错 + 选题
24. (2020八上·吴兴期末) 等腰Rt△ABC，点D为斜边AB上的中点，点E在线段BD上，连结CD，CE，作AH⊥CE，垂足为H，交CD于点G，AH的延长线交BC于点F.
1. （1）求证：△ADG≌△CDE.
2. （2）若点H恰好为CE的中点，求证：∠CGF=∠CFG.
答案解析收藏纠错 + 选题
25. (2022八下·惠州期末) 如图，直线l：y＝ $\text{[math]}$ x+b过点A（﹣3，0），与y轴交于点B，∠OAB的平分线交y轴于点C，过点C作直线AB的垂线，交x轴于点E，垂足是点D．
1. （1）求点B和点C的坐标；
2. （2）求直线DE的函数关系式；
3. （3）设点P是y轴上一动点，当PA+PD的值最小时，请直接写出点P的坐标．
答案解析收藏纠错 + 选题
26. (2020八上·邳州期末) 甲、乙两地间的直线公路长为 $\text{[math]}$ 千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行，货车比轿车早出发 $\text{[math]}$ 小时，途中轿车出现了故障，停下维修，货车仍继续行驶. $\text{[math]}$ 小时后轿车故障被排除，此时接到通知，轿车立刻掉头按原路原速返回甲地（接到通知及掉头时间不计）.最后两车同时到达甲地，已知两车距各自出发地的距离 $\text{[math]}$ （千米）与轿车所用的时间 $\text{[math]}$ （小时）的关系如图所示，请结合图象解答下列问题：
1. （1）货车的速度是千米/小时；轿车的速度是千米/小时； $\text{[math]}$ 值为.
2. （2）求轿车距其出发地的距离 $\text{[math]}$ （千米）与所用时间 $\text{[math]}$ （小时）之间的函数关系式并写出自变量 $\text{[math]}$ 的取值范围；
3. （3）请直接写出货车出发多长时间两车相距 $\text{[math]}$ 千米.
答案解析收藏纠错 + 选题
27. (2022八上·龙湖期中) 通过对下面数学模型的研究学习，解决下列问题：
1. （1）【模型呈现】
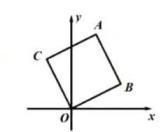
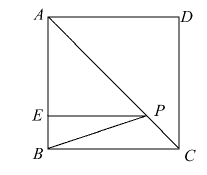
  如图1，∠BAD＝90°，AB＝AD，过点B作BC⊥AC于点C，过点D作DE⊥AC于点E．由∠1+∠2＝∠2+∠D＝90°，得∠1＝∠D．又∠ACB＝∠AED＝90°，可以推理得到△ABC≌△DAE．进而得到AC＝，BC＝．我们把这个数学模型称为“K字”模型或“一线三等角”模型；
2. （2）【模型应用】
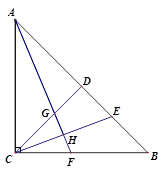
  如图2，∠BAD＝∠CAE＝90°，AB＝AD，AC＝AE，连接BC，DE，且BC⊥AF于点F，DE与直线AF交于点G．求证：点G是DE的中点；
3. （3）如图3，在平面直角坐标系xOy中，点A的坐标为（2，6），点B为平面内任一点．若△AOB是以OA为斜边的等腰直角三角形，请直接写出点B的坐标．
答案解析收藏纠错 + 选题