安徽省滁州市定远县吴圩片2021-2022学年八年级下学期5...

更新时间：2023-02-13 浏览次数：37 类型：月考试卷

一、单选题

1. (2023八上·平桥开学考) 实数 $\text{[math]}$ 在数轴上对应点的位置如图所示，且 $\text{[math]}$ ，则化简 $\text{[math]}$ 的结果为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022八下·定远月考) 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . -1 D . 1

答案解析收藏纠错 + 选题
3. (2024八下·萧山期中) 关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 化为一般形式后不含一次项，则 $\text{[math]}$ 的值为（）

A . 0 B . $\text{[math]}$ C . 3 D . -3

答案解析收藏纠错 + 选题
4. (2024九下·银川月考) 如果关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有实数根，那么 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ 且 $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 且 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022八下·定远月考) 如图，在长为80米，宽为60米的矩形场地上修建两条宽度相等且互相垂直的道路，剩余部分进行绿化，要使绿化面积为 $\text{[math]}$ ，则道路的宽应为多少米？设道路的宽为x米，则可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023八上·内江期末) 已知Rt $\text{[math]}$ ABC中，∠ACB＝90°，AC＝BC，AB＝4 $\text{[math]}$ ，D为BC的中点，E是线段AB上一点，连接CE、DE，则CE+DE的最小值是（）

A . 2 $\text{[math]}$ B . 2 $\text{[math]}$ C . 4 $\text{[math]}$ D . 2+2 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023八下·绥宁期中) 如图，长方形纸片ABCD中，AB=3cm，AD=9cm，将此长方形纸片折叠，使点D与点B重合，点C落在点H的位置，折痕为EF ，则△ABE的面积为（）

A . 6cm² B . 8cm² C . 10cm² D . 12cm²

答案解析收藏纠错 + 选题
8. (2022八下·定远月考) 已知实数a，b，c，是 $\text{[math]}$ 三边的长，且满足等式 $\text{[math]}$ ， $\text{[math]}$ ，则关于 $\text{[math]}$ 的形状最准确的描述是（）

A . 等边三角形 B . 等腰三角形 C . 直角三角形 D . 等腰直角三角形

答案解析收藏纠错 + 选题
9. (2022八下·定远月考) 如图，在四边形ABCD中，∠A=140°，∠D=90°，OB平分∠ABC，OC平分∠BCD，则∠BOC=(　　)

A . 105° B . 115° C . 125° D . 135°

答案解析收藏纠错 + 选题
10. (2022八下·定远月考) 如图，在 $\text{[math]}$ 中，点E，F分别在边AB，AD上，将△AEF沿EF折叠，点A恰好落在BC边上的点G处，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则AF长度为（）

A . $\text{[math]}$ B . 7 C . 6 D . 20

答案解析收藏纠错 + 选题

二、填空题

11. (2022八下·定远月考) 函数 $\text{[math]}$ 的自变量 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
12. (2022八下·定远月考) 若关于x的一元二次方程 $\text{[math]}$ 的一个实数根是 $\text{[math]}$ ，则m的值为．

答案解析收藏纠错 + 选题
13. (2023八下·江油月考) 在《九章算术》中有一个问题（如图)：今有竹高一丈，末折抵地，去本三尺，问折者高几何?它的意思是：一根竹子原高一丈（ $\text{[math]}$ 尺)，中部一处折断，竹梢触地面处离竹根 $\text{[math]}$ 尺，试问折断处离地面尺．

答案解析收藏纠错 + 选题
14. (2022八下·定远月考) 将等边三角形、正方形、正五边形按如图所示的位置摆放．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题

三、解答题

15. (2022八下·定远月考)
1. （1）已知： $\text{[math]}$ ，求yx．
2. （2）已知 $\text{[math]}$ ，求x²y+xy²的值．
答案解析收藏纠错 + 选题
16. (2023·柯桥模拟) 如图1，图2分别是某种型号拉杆箱的实物图与示意图，根据商品介绍，获得了如下信息：滑竿DE、箱长BC拉杆AB的长度都相等，即DE=BC=AB=50，点B、F在线段AC上，点C在DE上，支杆DF=30cm．
1. （1）若EC=36cm时，B，D相距48cm，试判定BD与DE的位置关系，并说明理由；
2. （2）当∠DCF＝45°，CF＝ $\text{[math]}$ AC时，求CD的长．
答案解析收藏纠错 + 选题
17. (2022八下·定远月考) 如图，在正方形网格中，每个小正方形的边长为1．
1. （1）在图中画出以AC为对角线的平行四边形ABCD；
2. （2）写出D的坐标和平行四边形ABCD的面积．
答案解析收藏纠错 + 选题
18. (2022八下·定远月考) 我们已经学习了利用配方法解一元二次方程，其实配方法还有其他重要应用．
例：已知 $\text{[math]}$ 可取任何实数，试求二次三项式 $\text{[math]}$ 最小值．
解： $\text{[math]}$
$\text{[math]}$
$\text{[math]}$ 无论 $\text{[math]}$ 取何实数，总有 $\text{[math]}$ ．
$\text{[math]}$ ，即 $\text{[math]}$ 的最小值是-10．
即无论 $\text{[math]}$ 取何实数， $\text{[math]}$ 的值总是不小于-10的实数．
1. （1）问题：
  已知 $\text{[math]}$ ，求证 $\text{[math]}$ 是正数．
2. （2）知识迁移：
  如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，从点 $\text{[math]}$ 向点 $\text{[math]}$ 以 $\text{[math]}$ 的速度移动，点 $\text{[math]}$ 在 $\text{[math]}$ 边上以 $\text{[math]}$ 的速度从点 $\text{[math]}$ 向点 $\text{[math]}$ 移动．若点 $\text{[math]}$ ， $\text{[math]}$ 同时出发，且当一点移动到终点时，另一点也随之停止，设 $\text{[math]}$ 的面积为 $\text{[math]}$ ，运动时间为 $\text{[math]}$ 秒，求 $\text{[math]}$ 的最大值．
答案解析收藏纠错 + 选题
19. (2022八下·定远月考) 已知关于x的一元二次方程 $\text{[math]}$ .
1. （1）若方程的一个根为 $\text{[math]}$ ，求a的值；
2. （2）若方程有实数根，求满足条件的正整数a的值.
答案解析收藏纠错 + 选题
20. (2022八下·定远月考) 如图，田村有一口呈四边形的池塘，在它的四个角A、B、C、D处均种有一棵大核桃树．田村准备开挖池塘建养鱼池，想使池塘面积扩大一倍，又想保持核桃树不动，并要求扩建后的池塘成平行四边形的形状，请问田村能否实现这一设想？若能，请你设计并画出图形；若不能，请说明理由（画图要保留痕迹，不写画法）．

答案解析收藏纠错 + 选题
21. (2022八下·定远月考) 我们根据图形的移、拼、补可以简单直观地推理验证数学规律和公式，这种方法称之为“无字证明”，它比严谨的数学证明更为优雅与有条理．下面是用三块全等的直角三角形移、拼、补所形成的“无字证明”图形．
1. （1）此图可以用来证明你学过的什么定理？请写出定理的内容；
2. （2）已知直角三角形直角边长分别为a、b，斜边长为c，图1、图2的面积相等，请你根据此图证明（1）中的定理．
答案解析收藏纠错 + 选题
22. (2023九上·仙居开学考) 【问题提出】在2020年抗击新冠肺炎的斗争中，某中学响应政府“停课不停学”的号召进行线上学习，七年级一班的全体同学在自主完成学习任务的同时，全班每两个同学都通过一次视频电话，彼此关怀，互相勉励，共同提高，若每两名同学之间仅通过一次视频电话，如何求全班50名同学共通过多少次电话呢？
【模型构建】用点M₁、M₂、M₃、…、M₅₀分别表示第1、2、3、…、50名同学，把该班级人数n与视频通话次数S之间的关系用如图模型表示：
1. （1）【问题解决】
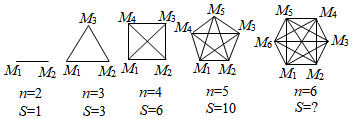
  填写如图中第5个图中S的值为．
2. （2）通过探索发现，通电话次数S与该班级人数n之间的关系式为，则当n＝50时，对应的S＝．
3. （3）若该班全体女生相互之间共通话190次，求该班共有多少名女生？
4. （4）【问题拓展】
  若该班数学兴趣小组的同学，每两位同学之间互发一条微信问候，小明统计全组共发送微信110条，则该班数学兴趣小组的人数是人．
答案解析收藏纠错 + 选题
23. (2022八下·定远月考) 如图，在四边形ABCD中，AB∥CD，∠ADC＝90°，E为BC的中点，连接DE并延长，与AB的延长线交于点F，连接BD、FC．
1. （1）求证：四边形BFCD是平行四边形；
2. （2）连接AE，若CD＝2，AD＝3，AB＝4，求AE的长．
答案解析收藏纠错 + 选题