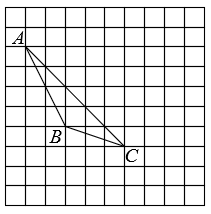

( 1 )在给定方格纸中画出平移后的△A'B'C';
( 2 )画出AB边上的中线CD;
( 3 )画出BC边上的高线AE;
( 4 )△A'B'C'的面积为 ▲ ;
( 5 )在图中能使S△PAC=S△ABC的格点P的个数有 ▲ 个(点P异于点B).
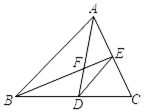

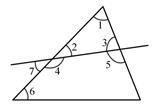
①若 ,
, 则
▲ ;
②若 , 则
▲ ;
③探究与
之间的数量关系,说明理由;

 D .
D . 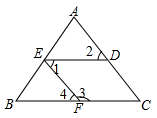
 B .
B .  C .
C .  D .
D .