 B .
B .  C .
C .  D .
D . 
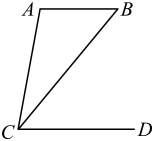
 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 
甲 | 100 | 102 | 99 | 101 | 98 |
乙 | 100 | 97 | 104 | 97 | 102 |
那么包装机包装的5袋糖果的质量比较稳定(填“甲”或“乙”).
![]()
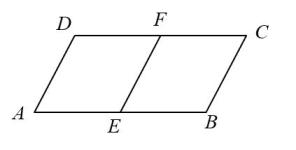
求作:△ABC,使得 ,
.
作法:①在射线AM上任取一点O(不与点A重合);
②以点O为圆心,OA长为半径画弧,交射线AM于A,C两点;
③以点C为圆心,CO长为半径画弧,交于点B;
④连接AB,BC.
△ABC就是所求作的三角形.
证明:连接OB.
在⊙O中,OB=OC
在⊙C中,OC==BC
∴OB=OC=BC
∴△OCB是等边三角形
∴
∵AC是⊙O的直径,
∴∠ABC= ▲ °( )(填推理的依据).
∴
∴ .
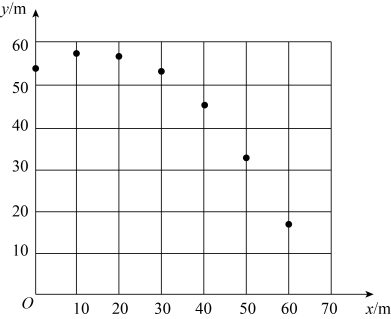
x/m | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
y/m | 54.0 | 57.8 | 57.6 | 53.4 | 45.2 | 33.0 | 16.8 |
下面是小明的探究过程,请补充完整:
a.该校七年级抽取的学生测试成绩的数据的频数分布直方图如下(数据分为5组 ,
,
,
,
)
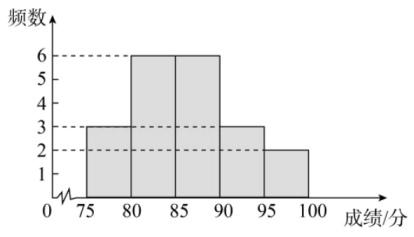
b.该校七年级抽取的学生测试成绩的数据在这一组的是:85;85;85;86;87;88
c.该校七、八年级抽取的学生的测试成绩的数据的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 | |
七年级 | 85.2 | m | 85 |
八年级 | 87 | 89.5 | 90 |
根据以上信息,回答下列问题:
①记该校七年级抽取的学生中成绩优秀的人数是 , 八年级抽取的学生中成绩优秀的人数为
, 比较
,
的大小,并说明理由;
②该校七、八年级各有200名学生,假设该校七、八年级学生全部参加此次测试,请估计成绩优秀的学生总人数(直接写出结果).
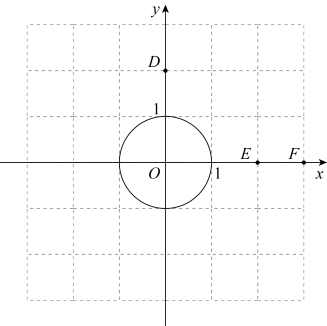
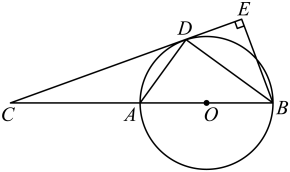
①d(D,⊙O)= ▲ ;
②若点M在线段EF上,求d(M,⊙O)的取值范围;