山东省济南市历下区五校联考2022-2023学年九年级下学期...

更新时间：2023-04-19 浏览次数：49 类型：月考试卷

一、单选题

1. (2023九下·历下月考) $\text{[math]}$ 的倒数是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023九下·历下月考) 下列几何体中，俯视图为三角形的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023九下·历下月考) 中国移动数据中心IDC项目近日在高新区正式开工建设，该项目规划建设规模12.6万平方米，建成后将成为山东省最大的数据业务中心．其中126000用科学记数法表示应为（）

A . 1.26×10⁶ B . 12.6×10⁴ C . 0.126×10⁶ D . 1.26×10⁵

答案解析收藏纠错 + 选题
4. (2022·历下月考)
如图，将直尺与含30°角的三角尺摆放在一起，若∠1=20°，则∠2的度数是（）

A . 50° B . 60° C . 70° D . 80°

答案解析收藏纠错 + 选题
5. (2023九下·历下月考) 下列图形中，既是轴对称图形又是中心对称图形的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2022·历下月考) 下列运算中，计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九下·章丘模拟) 若方程x²−cx+4=0有两个不相等的实数根，则c的值不可能是（）

A . 10 B . 6 C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022·历下月考) 若 $\text{[math]}$ ，则正比例函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 在同一平面直角坐标系中的大致图像可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2022·历下月考) 如图，在矩形 $\text{[math]}$ 按以下步骤作图：①分别以点A和C为圆心，以大于 $\text{[math]}$ 的长为半径作弧，两弧相交于点M和N；②作直线 $\text{[math]}$ 交 $\text{[math]}$ 于点E；③连接 $\text{[math]}$ ， $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024九下·赣榆模拟) 在平面直角坐标系中，对于点 $\text{[math]}$ 和点 $\text{[math]}$ ，给出如下新定义，若 $\text{[math]}$ ，则称点 $\text{[math]}$ 是点 $\text{[math]}$ 的限变点，例如：点 $\text{[math]}$ 的限变点是 $\text{[math]}$ ，点 $\text{[math]}$ 的限变点是 $\text{[math]}$ ，若点 $\text{[math]}$ 在二次函数 $\text{[math]}$ 的图象上，则当 $\text{[math]}$ 时，其限变点 $\text{[math]}$ 的纵坐标 $\text{[math]}$ 的取值范围是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2024八下·锦江期末) 分解因式： $\text{[math]}$ =

答案解析收藏纠错 + 选题
12. (2023·平房模拟) 一个不透明的袋子中装有3个小球，其中2个红球，1个绿球，这些小球除颜色外无其他差别，从袋子中随机摸出一个小球，则摸出的小球是红球的概率为．

答案解析收藏纠错 + 选题
13. (2022·历下月考) 方程 $\text{[math]}$ 的解为．

答案解析收藏纠错 + 选题
14. (2023·平阴模拟) 如图，将一个正六边形与一个正五边形如图放置，顶点A、B、C、D四点共线，E为公共顶点．则∠BEC＝．

答案解析收藏纠错 + 选题
15. (2022·历下月考) 小泽和小帅两同学分别从甲地出发，骑自行车沿同一条路到乙地参加社会实践活动．如图折线 $\text{[math]}$ 和线段 $\text{[math]}$ 分别表示小泽和小帅离甲地的距离y（单位：千米）与时间x（单位：小时）之间函数关系的图象，则当小帅到达乙地时，小泽距乙地的距离为千米．

答案解析收藏纠错 + 选题
16. (2022·历下月考) 如图，矩形纸片 $\text{[math]}$ ， $\text{[math]}$ ，点E，F分别在 $\text{[math]}$ ， $\text{[math]}$ 上，把纸片如图沿 $\text{[math]}$ 折叠，点A，B的对应点分别为 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ 并延长交线段 $\text{[math]}$ 于点G，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题

三、解答题

17. (2022·历下月考) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2022·历下月考) 解不等式组： $\text{[math]}$ ，并写出它的正整数解．

答案解析收藏纠错 + 选题
19. (2023九下·历下月考) 如图，点E是正方形 $\text{[math]}$ 内一点， $\text{[math]}$ 是等边三角形，连接 $\text{[math]}$ ．求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2023九下·历下月考) 某校为调查学生对海洋科普知识的了解情况，从全校学生中随机抽取n名学生进行测试，测试成绩进行整理后分成五组，并绘制成如图的频数分布直方图和扇形统计图．
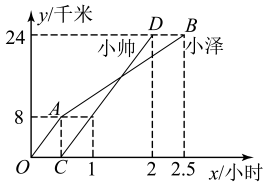
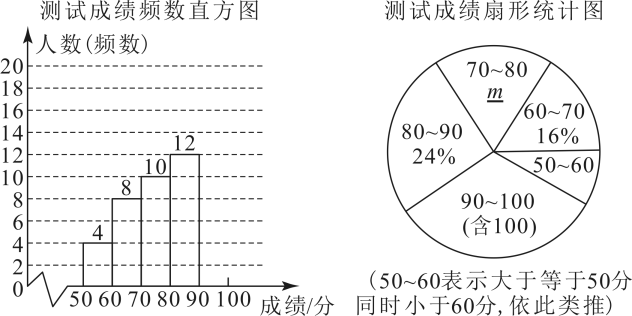
请根据图中信息解答下列问题：
1. （1）补全频数分布直方图；
2. （2）在扇形统计图中，“ $\text{[math]}$ ”这组的百分比m=；
3. （3）已知“ $\text{[math]}$ ”这组的数据如下：83，85，87，81，86，84，88，85，86，86，88，89．这组数据的众数是分；抽取的n名学生测试成绩的中位数是分；
4. （4）若成绩达到80分以上（含80分）为优秀，请你估计全校1200名学生对海洋科普知识了解情况为优秀的学生人数．
答案解析收藏纠错 + 选题
21. (2023九下·历下月考) 如图， $\text{[math]}$ 为 $\text{[math]}$ 的直径， $\text{[math]}$ 切 $\text{[math]}$ 于E， $\text{[math]}$ 于C，交 $\text{[math]}$ 于D．
1. （1）求证： $\text{[math]}$ 平分 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的半径．
答案解析收藏纠错 + 选题
22. (2023九下·历下月考) 某学校教学楼（甲楼）的顶部E和大门A之间挂了一些彩旗．小颖测得大门A距甲楼的距离 $\text{[math]}$ 是 $\text{[math]}$ ，在A处测得甲楼顶部E处的仰角是31°．
1. （1）求甲楼的高度；
2. （2）若小颖在甲楼楼底C处测得学校后面医院楼（乙楼）楼顶G处的仰角为 $\text{[math]}$ ，爬到甲楼楼顶F处测得乙楼楼顶G处的仰角为 $\text{[math]}$ ，求甲乙两楼之间的距离．（结果带根号）（ $\text{[math]}$ ． $\text{[math]}$ ．）
答案解析收藏纠错 + 选题
23. (2023八上·苍溪期末) 2022年10月16日，习总书记在第二十次全国代表大会上的报告中提出：“积极稳妥推进碳达峰碳中和”．某公司积极响应节能减排号召，决定采购新能源A型和B型两款汽车，已知每辆A型汽车的进价是每辆B型汽车的进价的1.5倍，若用3000万元购进A型汽车的数量比2400万元购进B型汽车的数量少20辆．
1. （1） A型和B型汽车的进价分别为每辆多少万元？
2. （2）该公司决定用不多于3600万元购进A型和B型汽车共150辆，最多可以购买多少辆A型汽车？
答案解析收藏纠错 + 选题
24. (2023九下·历下月考) 正方形 $\text{[math]}$ 的边长为4， $\text{[math]}$ ， $\text{[math]}$ 交于点E．在点A处建立平面直角坐标系如图所示．
1. （1）如图（1），双曲线 $\text{[math]}$ 过点E，完成填空：点C的坐标是．点E的坐标是，双曲线的解析式是；
2. （2）如图（2），双曲线 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 分别交于点M，N（反比例图像不一定过点E）．求证 $\text{[math]}$ ；
3. （3）如图（3），将正方形 $\text{[math]}$ 向右平移 $\text{[math]}$ 个单位长度，使过点E的双曲线 $\text{[math]}$ 与 $\text{[math]}$ 交于点P．当 $\text{[math]}$ 是以 $\text{[math]}$ 为腰的等腰三角形时，求m的值．
答案解析收藏纠错 + 选题
25. (2024·高州模拟)
1. （1）【问题情境】如图1，四边形ABCD是正方形，点E是AD边上的一个动点，以CE为边在CE的右侧作正方形CEFG，连接DG、BE，则DG与BE的数量关系是；
2. （2）【类比探究】
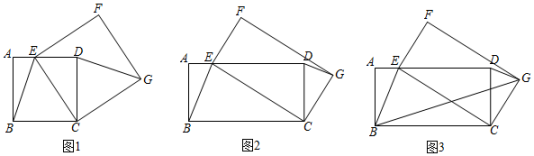
  如图2，四边形ABCD是矩形，AB=2，BC=4，点E是AD边上的一个动点，以CE为边在CE的右侧作矩形CEFG，且CG：CE=1：2，连接DG、BE．判断线段DG与BE有怎样的数量关系和位置关系，并说明理由；
3. （3）【拓展提升】
  如图3，在（2）的条件下，连接BG，则2BG+BE的最小值为．
答案解析收藏纠错 + 选题
26. (2023九下·历下月考) 抛物线 $\text{[math]}$ 过 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点．
1. （1）求抛物线的表达式；
2. （2）如图①，点K与点C关于抛物线对称轴对称，抛物线上一点D在线段AK的上方， $\text{[math]}$ 交AK于点E，若满足 $\text{[math]}$ ，求点D的坐标；
3. （3）如图②，F为抛物线顶点，过A作直线 $\text{[math]}$ ，若点P在直线l上运动，点Q在x轴上运动．是否存在这样的点P、Q，使得 $\text{[math]}$ 与 $\text{[math]}$ 相似（P与F为对应点），若存在，直接写出P、Q的坐标及此时 $\text{[math]}$ 的面积；若不存在，请说明理由．
答案解析收藏纠错 + 选题