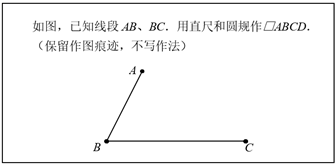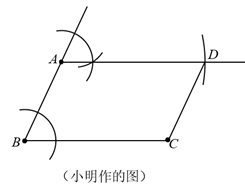
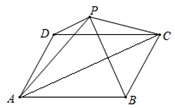


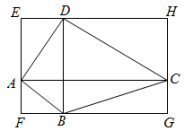
小明同学做法是:连接BD,利用三角形的中位线定理证明得出 , EH=FG,从而得到四边形EFGH是平行四边形.
请你完成小明的做法:
证明:连接BD,



|
平行四边形的性质定理3:行四边形的对角线互相平分。 我们可以用演绎推理证明这个结论。 已知:如图, 求证:OA=OC,OB=OD。
|
证明:

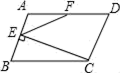
【性质应用】
如图2,的对角线
相交于点
,
过点
且与
分别相交于点
,
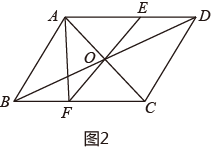

① ▲ °,构造的四边形是菱形;
②若构造的四边形是矩形,则不同的矩形应该有 ▲ 个.