人教版初中数学几何辅助线进阶训练——一般四边形的辅助线：连对...

如图1，在平面直角坐标系中，四边形OABC各顶点的坐标分别O(0，0)，A(3，3 )，B(9，5 )，C(14，0).动点P与Q同时从O点出发，运动时间为t秒，点P沿OC方向以1单位长度/秒的速度向点C运动，点Q沿折线OA−AB−BC运动，在OA，AB，BC上运动的速度分别为3， ， (单位长度/秒)﹒当P，Q中的一点到达C点时，两点同时停止运动．

四边形ABCD是正方形，AC与BD，相交于点O，点E、F是直线AD上两动点，且AE=DF，CF所在直线与对角线BD所在直线交于点G，连接AG，直线AG交BE于点H．

（1）如图1，当点E、F在线段AD上时，①求证：∠DAG=∠DCG；②猜想AG与BE的位置关系，并加以证明；

（2）如图2，在（1）条件下，连接HO，试说明HO平分∠BHG；

（3）当点E、F运动到如图3所示的位置时，其它条件不变，请将图形补充完整，并直接写出∠BHO的度数．

如图，在梯形ABCD中，AD∥BC，∠B=45°，∠C=120°，AD= ，BC=4 ，求CD的长．

【问题背景】

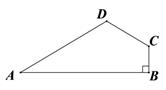
如图1，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，点E、F分别是边BC、CD上的点，且∠EAF＝60°，试探究图中线段BE、EF、FD之间的数量关系．

小王同学探究此问题的方法是：延长FD到点G，使GD＝BE，连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是      ▲       ．

【探索延伸】

如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°，点E、F分别是边BC、CD上的点，且∠EAF＝∠BAD，上述结论是否仍然成立，并说明理由．