题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

广东省茂名市高州市2022-2023学年七年级下学期5月月考...

更新时间：2023-06-23 浏览次数：65 类型：月考试卷

一、选择题（本大题共10小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项是正确的，请把正确答案代号填涂在答题卡相应位置上。）

1. (2024七下·柯桥期末) 下面计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八上·增城期末) 生物学家发现了一种病毒，其长度约为0.00000032mm，数据0.00000032用科学记数法表示正确的是（　　）

A . 3.2×10⁷ B . 3.2×10⁸ C . 3.2×10^-7 D . 3.2×10^-8

答案解析收藏纠错 + 选题
3. (2024七下·乐平期中) 如图所示，下列判断错误的是（）

A . 若∠1＝∠3，AD∥BC，则BD是∠ABC的平分线 B . 若AD∥BC，则∠1＝∠2＝∠3 C . 若∠3+∠4+∠C＝180°，则AD∥BC D . 若∠2＝∠3，则AD∥BC

答案解析收藏纠错 + 选题
4. (2023七下·榆阳期末) 如图，A ， B ， C ， D在同一条直线上， $\text{[math]}$ ， $\text{[math]}$ ，在下列条件中，不能使 $\text{[math]}$ 与 $\text{[math]}$ 全等的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023七下·高州月考) 若a，b，c是△ABC的三边，则化简 $\text{[math]}$ 的结果是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 0

答案解析收藏纠错 + 选题
6. (2023七下·高州月考) 如图，描述了某汽车在行驶过程中速度与时间的关系图，下列说法中错误的是（）

A . 第3分时汽车的速度是40千米/时 B . 第12分时汽车的速度是0千米/时 C . 从第3分到第6分，汽车行驶了120千米 D . 从第9分到第12分，汽车的速度从60千米/时减少到0千米/时

答案解析收藏纠错 + 选题
7. (2023七下·高州月考) 下列说法：①在同一平面内，不相交的两条线段叫做平行线；②过直线外一点，有且只有一条直线平行于已知直线；③两条平行直线被第三条直线所截，同位角相等；④同旁内角相等，两直线平行．其中正确的个数有（）个．

A . 4 B . 3 C . 2 D . 1

答案解析收藏纠错 + 选题
8. (2023七下·高州月考) 下列各式：①(x-2y)(2y+x)； ② (x-2y)(-x-2y)； ③ (-x-2y)(x+2y)； ④(x-2y)(-x+2y).
其中能用平方差公式计算的是（）

A . ①② B . ②③ C . ③④ D . ①④

答案解析收藏纠错 + 选题
9. (2023七下·高州月考) 如图， $\text{[math]}$ 的面积为20，点D ， E ， F分别为 $\text{[math]}$ 的中点，则阴影部分 $\text{[math]}$ 的面积为（）

A . 4 B . 5 C . 6 D . 10

答案解析收藏纠错 + 选题
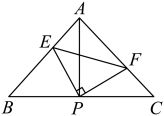
10. (2023八上·翁源月考) 如图，已知在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，直角 $\text{[math]}$ 的顶点P是 $\text{[math]}$ 的中点，两边 $\text{[math]}$ 、 $\text{[math]}$ 分别交 $\text{[math]}$ 、 $\text{[math]}$ 于点E、F.以下四个结论：① $\text{[math]}$ ；② $\text{[math]}$ 是等腰直角三角形；③ $\text{[math]}$ ；④ $\text{[math]}$ .其中正确的是（）

A . ①②③ B . ①②④ C . ②③④ D . ①②③④

答案解析收藏纠错 + 选题

二、填空题（本大题共5小题，每小题3分，共15分）

11. (2023八上·嘉祥月考) 已知 $\text{[math]}$ 是完全平方式，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2023七下·高州月考) 如图，在△ABC中，∠C=90°，AD平分∠BAC，AB=5，CD=2，则△ABD的面积是．

答案解析收藏纠错 + 选题
13. (2023七下·高州月考) 若 $\text{[math]}$ ，则m+n=；

答案解析收藏纠错 + 选题
14. (2023七下·高州月考) 一个三角形的两边长分别是2和7，最长边a为偶数，则这个三角形的周长为

答案解析收藏纠错 + 选题
15. (2023七下·高州月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 垂直平分 $\text{[math]}$ ，点 $\text{[math]}$ 为直线 $\text{[math]}$ 上的一个动点，则 $\text{[math]}$ 周长的最小值是。

答案解析收藏纠错 + 选题

三、解答题（一）（本大题共3小题，每小题8分，共24分）

16. (2023七下·高州月考) 计算：
1. （1）计算：－1²＋(－3)⁰－ $\text{[math]}$ ＋(－2)³
2. （2）计算： $\text{[math]}$ ；
答案解析收藏纠错 + 选题
17. (2023七下·章丘期末) 已知：如图， $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 互余， $\text{[math]}$ 于点 $\text{[math]}$ ，求证： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2023七下·高州月考) 如图，在正方形网格上有一个 $\text{[math]}$ ．
1. （1）画出 $\text{[math]}$ 关于直线 $\text{[math]}$ 的对称图形 $\text{[math]}$ （不写画法）；
2. （2）若网格上的每个小正方形的边长为1，求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题

四、解答题（二）（本大题3小题，每小题9分，共27分）

19. (2023七下·高州月考) 如图，在△ABC中，AB=AC，D、E是BC边上的点，连接AD，AE，以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E，连接D′C，若BD=CD′；
1. （1）求证：△ABD≌△ACD′；
2. （2）若∠BAC=120°，求∠DAE的度数。
答案解析收藏纠错 + 选题
20. (2023七下·高州月考) 小明用的练习本可以到甲超市购买，也可以到乙超市购买．已知两超市的标价都是每本1元，但甲超市的优惠条件是购买10本或少于10本按标价卖，10本以上，从第11本开始按标价的70%卖．乙超市的优惠条件是从第1本开始就按标价的85%卖．
1. （1）当小明要买28本时，到哪家超市购买较省钱？
2. （2）写出甲超市中，收款 $\text{[math]}$ (元)与购买本数x(本)的关系式．
3. （3）小明现有24元钱，最多可买多少本练习本？
答案解析收藏纠错 + 选题
21. (2023七下·高州月考) 如图，△ABC中，AB，AC的垂直平分线分别交BC于D，E两点，垂足分别是M，N.
1. （1）若△ADE的周长是10，求BC的长；
2. （2）若∠BAC＝100°，求∠DAE的度数．
答案解析收藏纠错 + 选题

五、解答题（三）（本大题2小题，每小题12分，共24分）

22. (2023七下·高州月考) 图1是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．
1. （1）图2中的阴影部分的正方形的边长等于 ▲ ，观察图2你能写出下列三个代数式(m+n)² ， (m-n)² ， mn之间的等量关系 ▲ ，运用你所得到的公式，计算若mn=-2，m-n=4，求 (m+n)²的值。
2. （2）已知 $\text{[math]}$ ，求 $\text{[math]}$ 值。
3. （3）用完全平方公式和非负数的性质求解：已知a、b、c是 $\text{[math]}$ 的三边长，满足 $\text{[math]}$ ，且c是 $\text{[math]}$ 最长的边，求c的取值范围。
答案解析收藏纠错 + 选题
23. (2024八上·寻乌期末) 如图（1）， $\text{[math]}$ =16cm， $\text{[math]}$ ， $\text{[math]}$ ，垂足分别为A ， B ， AC=10cm．点P在线段 $\text{[math]}$ 上以3cm/s的速度由点A向点B运动．同时，点Q在射线 $\text{[math]}$ 上运动．它们运动的时间为t（s）（当点P运动结束时，点Q运动随之结束）．
1. （1）若点Q的运动速度与点P的运动速度相等，当t=2时，
  ①试说明 $\text{[math]}$ ．
  
  ②此时，线段 $\text{[math]}$ 和线段 $\text{[math]}$ 有怎样的关系，请说明理由．
2. （2）如图（2），若“ $\text{[math]}$ ， $\text{[math]}$ ”改为“ $\text{[math]}$ ”，点Q的运动速度为xcm/s，其他条件不变，当点P ， Q运动到某处时，有 $\text{[math]}$ 和 $\text{[math]}$ 全等，求出此时的x ， t的值。
答案解析收藏纠错 + 选题

试卷信息