一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
-
-
-
4.
(2023高三下·浙江月考)
将正整数20分解成两个正整数的乘积有

,

,

三种,其中

是这三种分解中两数差的绝对值最小的.我们称

为20的最佳分解.当

(

且

)是正整数n的最佳分解时,定义函数

,则数列

的前100项和

为( )
-
5.
(2023高三下·浙江月考)
为调查中某校学生每天学习的时间,采用样本量比例分配的分层随机抽样,现抽取高一学生400人,其每天学习时间均值为8小时,方差为0.5,抽取高二学生600人,其每天学习时间均值为9小时,方差为0.8,抽取高三学生1000人,其每天学习时间均值为10小时,方差为1,则估计该校学生每天学习时间的方差为( )
A . 1.25
B . 1.35
C . 1.45
D . 1.55
-
6.
(2023高三下·浙江月考)
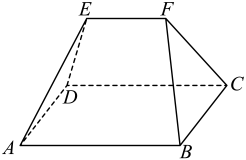
《九章算术》是我国古代著名的数学著作,其中记载有几何体“刍甍”.现有一个刍甍如图所示,底面

为正方形,

平面

, 四边形

为两个全等的等腰梯形,

, 且

, 则此刍甍体积的最大值为( )
-
-
A . 若 关于
关于 中心对称,则
中心对称,则 关于
关于 对称
B . 若
对称
B . 若 关于
关于 对称,则
对称,则 有对称中心
C . 若
有对称中心
C . 若 有1个对称中心和1条与
有1个对称中心和1条与 轴垂直的不过对称中心的对称轴,则
轴垂直的不过对称中心的对称轴,则 为周期函数
D . 若
为周期函数
D . 若 有两个不同的对称中心,则
有两个不同的对称中心,则 为周期函数
为周期函数
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对得5分,部分选对得2分,不选或有选错得0分.
三、填空题:本大题共4小题,每小题5分,共20分.
-
-
-
-
16.
(2023高三下·浙江月考)
在长方体

中,

, 过

且与直线

平行的平面

将长方体分成两部分,现同时将两个球分别放入这两部分几何体内,则在平面

变化的过程中,当两个球的半径之和达到最大时,此时较小球的表面积为
.
四、解答题:本题共6小题,共70.0分.解答题应写出文字说明、证明过程或演算步骤.
-
-
(1)
求

;
-
(2)
求

边上中线长的取值范围.
-
-
(1)
求数列

的通项;
-
-
-
-
(2)
当直线

与平面

所成角最小时,求二面角

的平面角的余弦值.
-
20.
(2023高三下·浙江月考)
为了解中学生的阅读情况,现随机抽取了某重点中学100人,调查他们是否喜爱阅读,统计人数如下表:
| 喜爱阅读 | 不喜爱阅读 | 共计 |
女生 | 45 | | 50 |
男生 | | 15 | |
共计 | | | |
-
(1)
根据

列联表中数据判断是否有

的把握认为“喜爱阅读与性别有关”?
-
(2)
现进行一项阅读答题测试,测试规则:若该同学连续三次答对,则测试通过,答题结束;若出现连续两次答错,则未通过测试,答题结束.其余情况下可以一直答题,直至出现前面两种情况.已知该同学每次答对的概率为

, 求该同学通过测试的概率.
参考附表:
 | 0.050 | 0.025 | 0.010 |
 | 3.841 | 5.024 | 6.635 |
参考公式: , 其中
, 其中
-
21.
(2023高三下·浙江月考)
已知椭圆

, 下顶点为

是椭圆上任意一点,过点

作

轴的平行线与直线

交于

点,若点

关于点

的对称点为

, 直线

交椭圆于

两点.
-
(1)
求椭圆

上点到直线

的距离的最大值;
-
(2)
已知

. 过点

作

垂直直线

, 垂足为

, 是否存在定点

, 使得

为定值,若存在求出定点

坐标和

, 若不存在,请说明理由.
-
-
(1)
试求

与

的公切线方程.
-
(2)
设

,
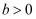
, 若不等式

对一切

恒成立,求

的最大值.

, 其中