|
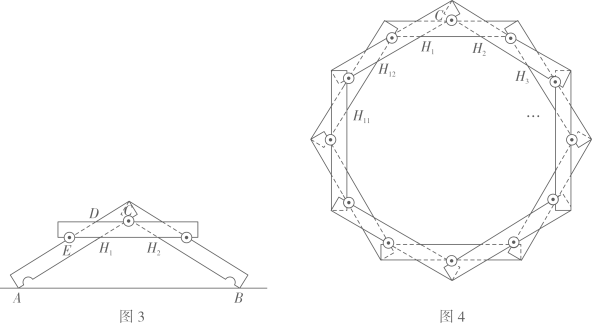
图1是搭成的“倍力桥”,纵梁a,c夹住横梁 图2是长为 |
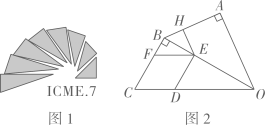
探究1:图3是“桥”侧面示意图,A,B为横梁与地面的交点,C,E为圆心,D,H1 , H2是横梁侧面两边的交点.测得AB=32cm,点C到AB的距离为12cm.试判断四边形CDEH1的形状,并求的值.
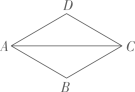
探究2:若搭成的“桥”刚好能绕成环,其侧面示意图的内部形成一个多边形.
①若有12根横梁绕成环,图4是其侧面示意图,内部形成十二边形 , 求
的值;
②若有n根横梁绕成的环(n为偶数,且n≥6),试用关于n的代数式表示内部形成的多边形的周长.