2023年中考数学真题分类汇编（全国版）：锐角三角函数（2）

更新时间：2023-07-23 浏览次数：157 类型：二轮复习

一、填空题

1. (2023·枣庄) 如图所示，桔棒是一种原始的汲水工具，它是在一根竖立的架子上加上一根细长的杠杆，末端悬挂一重物，前端悬挂水桶．当人把水桶放入水中打满水以后，由于杠杆末端的重力作用，便能轻易把水提升至所需处，若已知：杠杆 $\text{[math]}$ 米， $\text{[math]}$ ，支架 $\text{[math]}$ 米， $\text{[math]}$ 可以绕着点O自由旋转，当点A旋转到如图所示位置时 $\text{[math]}$ ，此时点B到水平地面 $\text{[math]}$ 的距离为米．（结果保留根号）

答案解析收藏纠错 + 选题
2. (2023·眉山) 一渔船在海上A处测得灯塔C在它的北偏东60°方向，渔船向正东方向航行12海里到达点B处，测得灯塔C在它的北偏东45°方向，若渔船继续向正东方向航行，则渔船与灯塔C的最短距离是海里．

答案解析收藏纠错 + 选题

二、计算题

3. (2023·邵阳) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
4. (2023·株洲) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023·内江) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023·扬州) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
7. (2023·广安) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023·眉山) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题

三、解答题

9. (2023·营口) 为了丰富学生的文化生活，学校利用假期组织学生到素质教育基地A和科技智能馆B参观学习，学生从学校出发，走到C处时，发现A位于C的北偏西 $\text{[math]}$ 方向上，B位于C的北偏西 $\text{[math]}$ 方向上，老师将学生分成甲乙两组，甲组前往A地，乙组前往B地，已知B在A的南偏西 $\text{[math]}$ 方向上，且相距1000米，请求出甲组同学比乙组同学大约多走多远的路程（参考数据： $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
10. (2023·张家界) “游张家界山水，逛七十二奇楼”成为今年旅游新特色．某数学兴趣小组用无人机测量奇楼 $\text{[math]}$ 的高度，测量方案如图：先将无人机垂直上升至距水平地面225m的P点，测得奇楼顶端A的俯角为 $\text{[math]}$ ，再将无人机沿水平方向飞行200m到达点Q，测得奇楼底端B的俯角为 $\text{[math]}$ ，求奇楼 $\text{[math]}$ 的高度．（结果精确到1m，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题

11. (2023·山西) 2023年3月，水利部印发《母亲河复苏行动河湖名单（2022－2025年）》，我省境内有汾河、桑干河、洋河、清漳河、浊漳河、沁河六条河流入选．在推进实施母亲河复苏行动中，需要砌筑洛种驳岸（也叫护坡）．某校“综合与实践”小组的同学把“母亲河驳岸的调研与计算”作为一项课题活动，利用课余时间完成了实践调查，并形成了如下活动报告．请根据活动报告计算 $\text{[math]}$ 和 $\text{[math]}$ 的长度（结果精确到 $\text{[math]}$ ．参考数据： $\text{[math]}$ ， $\text{[math]}$ ）。

课题	母亲河驳岸的调研与计算
调查方式	资料查阅、水利部门走访、实地查看了解
	功能	驳岸是用来保护河岸，阻止河岸崩塌或冲刷的构筑物
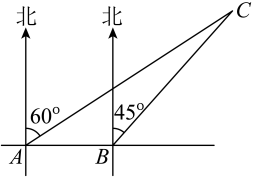
	驳岸剖面图		相关数据及说明，图中，点A，B，C，D，E在同一竖直平面内， $\text{[math]}$ 与 $\text{[math]}$ 均与地面平行，岸墙 $\text{[math]}$ 于点A， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
	计算结果
交流展示

答案解析收藏纠错 + 选题

12. (2023·新疆) 烽燧即烽火台，是古代军情报警的一种措施，史册记载，夜间举火称“烽”，白天放烟称“燧”．克孜尔尕哈烽燧是古丝绸之路北道上新疆境内时代最早、保存最完好、规模最大的古代烽燧（如图1）．某数学兴趣小组利用无人机测量该烽燧的高度，如图2，无人机飞至距地面高度 $\text{[math]}$ 米的A处，测得烽燧 $\text{[math]}$ 的顶部C处的俯角为 $\text{[math]}$ ，测得烽燧 $\text{[math]}$ 的底部B处的俯角为 $\text{[math]}$ ，试根据提供的数据计算烽燧 $\text{[math]}$ 的高度．（参数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
13. (2023·怀化) 为弘扬革命传统精神，清明期间，某校组织学生前往怀化市烈士陵园缅怀革命先烈．大家被革命烈士纪念碑的雄伟壮观震撼，想知道纪念碑的通高 $\text{[math]}$ （碑顶到水平地面的距离），于是师生组成综合实践小组进行测量．他们在地面的 $\text{[math]}$ 点用测角仪测得碑顶 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，在 $\text{[math]}$ 点处测得碑顶 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，已知 $\text{[math]}$ ，测角仪的高度是 $\text{[math]}$ （ $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 在同一直线上），根据以上数据求烈士纪念碑的通高 $\text{[math]}$ ．（ $\text{[math]}$ ，结果保留一位小数）

答案解析收藏纠错 + 选题
14. (2023·烟台) 风电项目对于调整能源结构和转变经济发展方式具有重要意义．某电力部门在一处坡角为 $\text{[math]}$ 的坡地新安装了一架风力发电机，如图1．某校实践活动小组对该坡地上的这架风力发电机的塔杆高度进行了测量，图2为测量示意图．已知斜坡 $\text{[math]}$ 长16米，在地面点 $\text{[math]}$ 处测得风力发电机塔杆顶端 $\text{[math]}$ 点的仰角为 $\text{[math]}$ ，利用无人机在点 $\text{[math]}$ 的正上方53米的点 $\text{[math]}$ 处测得 $\text{[math]}$ 点的俯角为 $\text{[math]}$ ，求该风力发电机塔杆 $\text{[math]}$ 的高度．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题

15. (2023·武威) 如图1，某人的一器官后面 $\text{[math]}$ 处长了一个新生物，现需检测到皮肤的距离（图1）．为避免伤害器官，可利用一种新型检测技术，检测射线可避开器官从侧面测量．某医疗小组制定方案，通过医疗仪器的测量获得相关数据，并利用数据计算出新生物到皮肤的距离．方案如下：

课题	检测新生物到皮肤的距离
工具	医疗仪器等
示意图
说明	如图2，新生物在 $\text{[math]}$ 处，先在皮肤上选择最大限度地避开器官的 $\text{[math]}$ 处照射新生物，检测射线与皮肤 $\text{[math]}$ 的夹角为 $\text{[math]}$ ；再在皮肤上选择距离 $\text{[math]}$ 处 $\text{[math]}$ 的 $\text{[math]}$ 处照射新生物，检测射线与皮肤 $\text{[math]}$ 的夹角为 $\text{[math]}$ ．
测量数据	$\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

请你根据上表中的测量数据，计算新生物 $\text{[math]}$ 处到皮肤的距离．（结果精确到 $\text{[math]}$ ）（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题

16. (2023·苏州) 四边形不具有稳定性，工程上可利用这一性质解决问题．如图是某篮球架的侧面示意图， $\text{[math]}$ 为长度固定的支架，支架在 $\text{[math]}$ 处与立柱 $\text{[math]}$ 连接（ $\text{[math]}$ 垂直于 $\text{[math]}$ ，垂足为 $\text{[math]}$ ），在 $\text{[math]}$ 处与篮板连接（ $\text{[math]}$ 所在直线垂直于 $\text{[math]}$ ）， $\text{[math]}$ 是可以调节长度的伸缩臂（旋转点 $\text{[math]}$ 处的螺栓改变 $\text{[math]}$ 的长度，使得支架 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转，从而改变四边形 $\text{[math]}$ 的形状，以此调节篮板的高度）．已知 $\text{[math]}$ ，测得 $\text{[math]}$ 时，点 $\text{[math]}$ 离地面的高度为 $\text{[math]}$ ．调节伸缩臂 $\text{[math]}$ ，将 $\text{[math]}$ 由 $\text{[math]}$ 调节为 $\text{[math]}$ ，判断点 $\text{[math]}$ 离地面的高度升高还是降低了？升高（或降低）了多少？（参考数据： $\text{[math]}$ ）

答案解析收藏纠错 + 选题

17. (2023·温州) 根据背景素材，探索解决问题.

测算发射塔的高度
背景素材	某兴趣小组在一幢楼房窗口测算远处小山坡上发射塔的高度MN（如图1）.他们通过自制的测倾仪（如图2）在A，B，C三个位置观测，测倾仪上的示数如图3所示.

	经讨论，只需选择其中两个合适的位置，通过测量﹑换算就能计算发射塔的高度.
问题解决
任务1	分析规划	选择两个观测位置：点 ▲ 和点 ▲ 。
	获取数据	写出所选位置观测角的正切值，并量出观测点之间的图上距离.
任务2	推理计算	计算发射塔的图上高度MN.
任务3	换算高度	楼房实际宽度DE为12米，请通过测量换算发射塔的实际高度.

注：测量时，以答题纸上的图上距离为准，并精确到1mm.

答案解析收藏纠错 + 选题

四、综合题

18. (2023·绍兴) 图1是某款篮球架，图2是其示意图，立柱 $\text{[math]}$ 垂直地面 $\text{[math]}$ ，支架 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，支架 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，支架 $\text{[math]}$ 平行地面 $\text{[math]}$ ，篮筐 $\text{[math]}$ 与支架 $\text{[math]}$ 在同一直线上， $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的度数.
2. （2）某运动员准备给篮筐挂上篮网，如果他站在凳子上，最高可以把篮网挂到离地面3米处，那么他能挂上篮网吗？请通过计算说明理由.
  （参考数据： $\text{[math]}$ ）
答案解析收藏纠错 + 选题
19. (2023·宁波) 某综合实践研究小组为了测量观察目标时的仰角和俯角，利用量角器和铅锤自制了一个简易测角仪，如图1所示．
1. （1）如图2，在 $\text{[math]}$ 点观察所测物体最高点 $\text{[math]}$ ，当量角器零刻度线上 $\text{[math]}$ 两点均在视线 $\text{[math]}$ 上时，测得视线与铅垂线所夹的锐角为 $\text{[math]}$ ，设仰角为 $\text{[math]}$ ，请直接用含 $\text{[math]}$ 的代数式示 $\text{[math]}$ ．
2. （2）如图3，为了测量广场上空气球 $\text{[math]}$ 离地面的高度，该小组利用自制简易测角仪在点 $\text{[math]}$ 分别测得气球 $\text{[math]}$ 的仰角 $\text{[math]}$ 为 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ ，地面上点 $\text{[math]}$ 在同一水平直线上， $\text{[math]}$ ，求气球 $\text{[math]}$ 离地面的高度 $\text{[math]}$ ．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ）
答案解析收藏纠错 + 选题
20. (2023·舟山) 图1是某住宅单元楼的人脸识别系统（整个头部需在摄像头视角围内才能被识别），其示意图如图2，摄像头A的仰角、俯角均为15°，摄像头高度 $\text{[math]}$ ，识别的最远水平距离 $\text{[math]}$ 。
1. （1）身高 $\text{[math]}$ 的小杜，头部高度为 $\text{[math]}$ ，他站在离摄像头水平距离 $\text{[math]}$ 的点C处，请问小杜最少需要下蹲多少厘米才能被识别。
2. （2）身高 $\text{[math]}$ 的小若，头部高度为 $\text{[math]}$ ，踮起脚尖可以增高 $\text{[math]}$ ，但仍无法被识别．社区及时将摄像头的仰角、俯角都调整为 $\text{[math]}$ （如图3），此时小若能被识别吗？请计算说明。
  （精确到 $\text{[math]}$ ，参考数据 $\text{[math]}$ ）
答案解析收藏纠错 + 选题
21. (2023·衡阳) 随着科技的发展，无人机已广泛应用于生产生活，如代替人们在高空测量距离和高度．圆圆要测量教学楼 $\text{[math]}$ 的高度，借助无人机设计了如下测量方案：如图，圆圆在离教学楼底部 $\text{[math]}$ 米的C处，遥控无人机旋停在点C的正上方的点D处，测得教学楼 $\text{[math]}$ 的顶部B处的俯角为 $\text{[math]}$ ， $\text{[math]}$ 长为 $\text{[math]}$ 米．已知目高 $\text{[math]}$ 为 $\text{[math]}$ 米．
1. （1）求教学楼 $\text{[math]}$ 的高度．
2. （2）若无人机保持现有高度沿平行于 $\text{[math]}$ 的方向，以 $\text{[math]}$ 米/秒的速度继续向前匀速飞行，求经过多少秒时，无人机刚好离开圆圆的视线 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
22. (2023·自贡) 为测量学校后山高度，数学兴趣小组活动过程如下：
1. （1）测量坡角
  如图1，后山一侧有三段相对平直的山坡 $\text{[math]}$ ，山的高度即为三段坡面的铅直高度 $\text{[math]}$ 之和，坡面的长度可以直接测量得到，要求山坡高度还需要知道坡角大小．
  如图2，同学们将两根直杆 $\text{[math]}$ 的一端放在坡面起始端A处，直杆 $\text{[math]}$ 沿坡面 $\text{[math]}$ 方向放置，在直杆 $\text{[math]}$ 另一端N用细线系小重物G，当直杆 $\text{[math]}$ 与铅垂线 $\text{[math]}$ 重合时，测得两杆夹角 $\text{[math]}$ 的度数，由此可得山坡AB坡角 $\text{[math]}$ 的度数．请直接写出 $\text{[math]}$ 之间的数量关系．
2. （2）测量山高
  同学们测得山坡 $\text{[math]}$ 的坡长依次为40米，50米，40米，坡角依次为 $\text{[math]}$ ；为求 $\text{[math]}$ ，小熠同学在作业本上画了一个含 $\text{[math]}$ 角的 $\text{[math]}$ （如图3），量得 $\text{[math]}$ ．求山高 $\text{[math]}$ ．（ $\text{[math]}$ ，结果精确到1米）
3. （3）测量改进
  由于测量工作量较大，同学们围绕如何优化测量进行了深入探究，有了以下新的测量方法．
  
  如图4，5，在学校操场上，将直杆NP置于 $\text{[math]}$ 的顶端，当 $\text{[math]}$ 与铅垂线 $\text{[math]}$ 重合时，转动直杆 $\text{[math]}$ ，使点N，P，D共线，测得 $\text{[math]}$ 的度数，从而得到山顶仰角 $\text{[math]}$ ，向后山方向前进40米，采用相同方式，测得山顶仰角 $\text{[math]}$ ；画一个含 $\text{[math]}$ 的直角三角形，量得该角对边和另一直角边分别为 $\text{[math]}$ 厘米， $\text{[math]}$ 厘米，再画一个含 $\text{[math]}$ 的直角三角形，量得该角对边和另一直角边分别为 $\text{[math]}$ 厘米， $\text{[math]}$ 厘米．已知杆高MN为 $\text{[math]}$ 米，求山高 $\text{[math]}$ ．（结果用不含 $\text{[math]}$ 的字母表示）
答案解析收藏纠错 + 选题