若
, 则
;
若
时,则
;
若点
,
, 在抛物线上,
, 且
, 则
;
当
时,关于x的一元二次方程
必有两个不相等的实数根.
如果
,
, 那么当
时,直线
与该二次函数有一个公共点,则
. 其中结论正确的个数有( )

①对于任意实数 ,
恒成立;
②若 , 则不等式
的解集是
;
③一元二次方程有一个根
;
④点 ,
在抛物线上,若
, 则当
时,总有
. 其中正确的是.(填写序号)
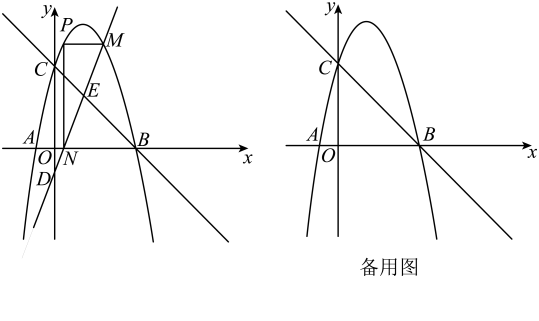
①求点的坐标;
②直接写出封闭图形的边界上的整点(横、纵坐标都是整数)的个数.