





如图1,经过A点可以作条对角线;同样,经过B点可以作条;经过C点可以作条;经过D点可以作条对角线.
通过以上分析和总结,图1共有条对角线.
运用(1)的分析方法,可得:
图2共有条对角线;
图3共有条对角线;
对于n边形(n>3),共有条对角线.(用含n的式子表示)
十边形有条对角线.
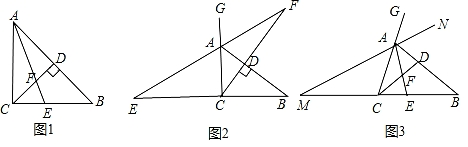
【习题回顾】已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
【变式思考】如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
【探究延伸】如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
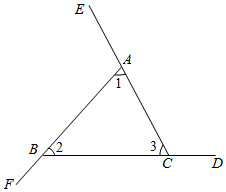
∠BAE、∠CBF、∠ACD是△ABC的三个外角.求证:∠BAE+∠CBF+∠ACD=360°
证法1:∵∠BAE、∠CBF、∠ACD是△ABC的三个外角
∴__▲_.
∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3)
∵_▲_.
∴∠BAE+∠CBF+∠ACD=360°
请把证法1补充完整,并用不同的方法完成证法2

解:∵∠ABC+∠ACB+∠A=180°(三角形内角和180° ).
∴∠ABC+∠ACB= ▲ (等式性质).
∵∠A=74° (已知),
∴∠ABC+∠ACB= ▲ (等量代换).
∵DB平分∠ABC(已知),
∴∠DBC=∠ABC(角平分线的定义).
同理,∠DCB= ▲ ;
∴(∠ABC+∠ACB)= ▲ (等式性质).
∵∠DBC+∠DCB+∠D=180°,
∴∠D=180°-(∠DBC+∠DCB)= ▲ (等式性质).
则∠D=( ).
如图1,已知点是
外一点,连接
,
, 求
的度数.
阅读并补充下面推理过程.
解:过点作
, 所以
,
又因为
所以
如图2,已知 , 求
的度数.
已知 , 点
在
的右侧,
,
平分
,
平分
,
,
所在的直线交于点
, 点
在
与
两条平行线之间.
①如图3,若 , 则
°
②如图4,点在点
的右侧,若
, 则
°(用含
的代数式表示)